Рассмотрим программу P.

С точки зрения разработчика, P состоит из набора подпрограмм (функций и/или процедур) и входной точки (в языке Си она называется main, в языке РЕФАЛ-5 - Go), которая, грубо говоря, находится в общем положении: то есть аргументы входной точки могут быть произвольны. Например, <Go e.x>. Здесь e.x - "переменная" (см. уточнение ниже), которая может принять в качестве значения любое данное языка РЕФАЛ, а угловые скобки означают вызов функции. Разработчик реализует программу для широкого круга пользователей.

С точки зрения конкретного пользователя, входная точка программы является полностью фиксированной. Чтобы запустить P, пользователь должен задать конкретные значения аргументов входной точки. В нашем случае: <Go e.x0>.

Специализатор программ находится между разработчиком и пользователем. В первом приближении это означает, что входная точка программы P частично задана, а частично неизвестна. Например, <Go ('string') e.x>.

Наша оговорка "в первом приближении" существенна: здесь есть много тонкостей, некоторые из которых мы рассмотрим в этой заметке; к более сложным, возможно, вернёмся позже. Однако, принципиальный момент мы уже отметили: для того чтобы запустить суперкомпилятор, недостаточно подать ему на вход преобразуемую программу; нужно еще поставить задачу специализации этой программы. Язык постановки таких задач В. Ф. Турчин назвал языком MST-схем (см., например, V. F. Turchin, A. P. Nemytykh. Metavariables: their Implementation and Use in Program Transformation. The City College of the City University of New York, Report N. TR 2095-012, 1995, 34 p. ).

Обратим внимание на следующее: наше описание задачи
<Go ('string') e.x> не вполне корректно. Любой язык программирования предполагает, что переменная принимает своё значение в процессе интерпретации программы. Мы же предполагаем, что e.x уже заданное входное значение, но для нас оно неизвестно. Если читатель когда-то в школе решал квадратные уравнения с параметром, то он вспомнит, что переменные в процессе решения такого уравнения также должны принять какие-то значения, а значения параметров уравнения хотя и заданы, но неизвестны школьнику: он вынужден рассматривать всевозможные значения параметров и в зависимости от их свойств выписывать решения уравнения. Разным параметрам могут соответствовать разные решения уравнения (значения переменных, при которых уравнение обращается в тождество).

В наших заметках мы ещё неоднократно будем обращаться к этому школьному примеру. Здесь же подытожим сказанное: суперкомпилятор должен уметь различать переменные и параметры. Первое уточнение нашей задачи на специализацию (MST-схемы): <Go ('string') #e.x> . Мы ввели синтаксическое понятие параметра, обозначив его приставкой #.

Итак, для постановки задач на специализацию программ возникает необходимость в языке параметров. Как этот язык связан, например, с языком описания переменных в языке программирования, программы на котором мы хотим специализировать? Выше, на примере, мы показали как мог бы быть определен простейший язык параметров: каждый тип переменных определяет соответствующий тип параметров. Насколько выразителен этот простейший язык? Посредством его можно описывать несложные задачи специализации, но, например, нельзя адекватно сформулировать классическую задачу специализации интерпретатора по данной программе. Если рассмотреть аналог такого простейшего языка параметров в Haskell, тогда, например, нельзя сформулировать задачу доказательства факта конечности времени работы данной программы (написанной на языке Haskell) на любых её входных данных - как задачу специализации.

Выбор языка параметров критичен не только с точки зрения формулировки задач на специализацию, но и с точки зрения получения удовлетворительного результата специализации. Это нетрудно понять: любой специализатор, по существу, сводит стартовую задачу специализации к последовательности промежуточных задач специализации, которые также описываются посредством выбранного языка параметров.

Рассмотрим прямую интерпретацию языков программирования. Примером может служить оболочка операционной системы Linux (shell). В shell входной точкой (командой, запросом) является любая строка, удовлетворяющая определенным синтаксическим правилам. Т.е. язык описания входных точек намного более выразителен, чем в Си или РЕФАЛе. Например, его синтаксис позволяет описать вызов композиции функций. В языке MST-схем также можно описывать подобные синтаксические конструкции. MST-схема <F #e.y <G #e.x>> ставит следующую задачу специализации программы P, в которой определены функции F и G: проспециализировать P, если известно, что P будет использоваться только посредством вызова указанной выше композиции функций G и F.

О некоторых других тонкостях, связанных с постановкой задач на специализацию, неподготовленный читатель может ознакомиться, например, здесь. На странице описано несколько простых примеров задач специализации, ознакомившись с которыми читатель может просуперкомпилировать эти примеры непосредственно с этой электронной страницы.

Вернёмся к нашему основному примеру - квадратному уравнению (см. предыдущую заметку).

Рассмотрим алгоритм его решения U. Если коэффициенты уравнения полностью известны (являются действительными числами), то алгоритм U однозначно определяет последовательность действий, которая приведёт либо к вычислению действительных корней данного уравнения, либо к выяснению факта отсутствия таких корней (т.е. к состоянию "аварийной остановки").

Другой школьный алгоритм _μU, позволяющий решать квадратные уравнения с параметрами, является метарасширением алгоритма U. Некоторые из коэффициентов уравнения могут быть известны, а некоторые заданы параметрами: т.е. хотя и заданы, но неизвестны. Известно лишь, что это какие-то действительные числа, но неизвестно какие именно. В соответствии с этим, в процессе решения квадратного уравнения с параметрами строится конечное дерево Г, узлы которого являются точками ветвления параметров (if, case). Ребра дерева Г помечены предикатами - условиями, уточняющими (сужающими) значения параметров таким образом, чтобы можно было однозначно проделать несколько действий первого алгоритма U равномерно по значениям параметров - до следующей точки ветвления. На листах дерева Г написаны параметризованные значения корней решаемого уравнения. Композиция последовательности предикатов от корня Г к листу определяет условие, при котором заданное уравнение имеет корни, помечающие этот лист. Итак, результатом алгоритма _μU является дерево Г и это дерево определено в терминах параметров.

Заметим, что (1) Г может оказаться пустым (при любых значениях параметров уравнение не имеет корней); (2) иначе корень этого дерева помечен уравнением (описанием постановки задачи).

Если условно считать, что школьник выполняет каждое арифметическое действие над действительными числами за единицу времени независимо ни от длины этих чисел, ни от других их свойств, тогда алгоритмы U и _μU можно описать, не используя программистского понятия цикла. Дерево Г всегда является конечным деревом.

Таким образом, о понятии прогонки читателю рассказывал в средней школе его учитель математики, к счастью, не произнося само слово "прогонка"; выше мы только напомнили читателю это понятие.

Еще раз перескажем то же самое, но теперь уже в программистских терминах.

Пусть дан некоторый алгоритмически полный язык программирования L. Алгоритм любого интерпретатора Int языка L описывается текстом конечной длины. Это простое замечание приводит нас к следующей структуре интерпретатора Int:

Int(p,d) {
   инициализация;
   while (вычисления не завершены)
         { STEP; }
   return (результирующее состояние);
}

Здесь STEP суть минимальный логически замкнутый шаг, включающий в себя все механизмы необходимые для интерпретации любой L-программы p на любых входных данных d. STEP изменяет глобальное состояние интерпретатора, которое и является аргументом STEP. В данной выше схеме этот аргумент явно не указан. Если физическое время T вычисления STEP равномерно ограничено по размеру его входных данных, тогда число шагов, необходимое для вычисления p на d, можно рассматривать как логическое время вычислений, которое адекватно отражает соответствующее физическое время вычислений. В более технических терминах условие равномерной ограниченности T означает отсутствие в STEP проходов по кускам его входных данных, размер которых (кусков) неизвестен разработчику интерпретатора Int, но при каждом конкретном запуске Int, конечно, может быть известен пользователю.

Одним из базовых механизмов суперкомпиляции является прогонка данной параметризованной конфигурации (параметризованного состояния стека вызовов функций специализируемой L-программы). Алгоритм прогонки является метарасширением интерпретации одного шага L-машины, преобразующего данное конкретное состояние стека вызовов в следующее конкретное состояние стека вызовов. Результатом прогонки является конечное дерево возможных вычислений данного на входе прогонки параметризованного (т.е. частично неизвестного) стека вызовов функций. Ниже мы будем называть это дерево гроздью прогонки, чтобы отличать его от других деревьев, возникающих в процессе суперкомпиляции.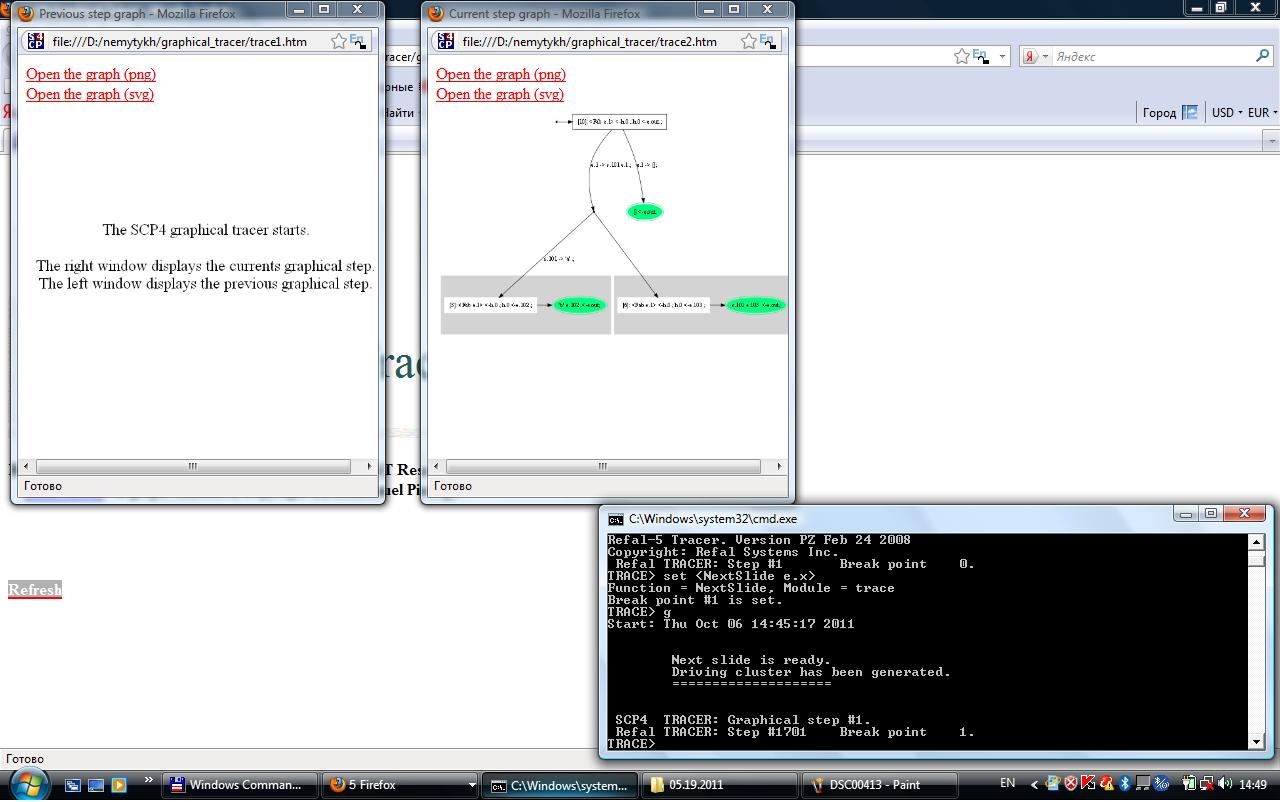

Рисунок 1. Результат первого вызова прогонки.

Рисунок 2. Результат первого вызова прогонки (крупный масштаб).

На Рисунках №1 и №2 показан пример снимков экрана (в разных масштабах) с результатом первого вызова алгоритма прогонки. Изображение построено графическим трассировщиком суперкомпилятора SCP4. Серые кластеры показывают структуры параметризованных стеков в листьях грозди прогонки. Зеленым цветом отмечены полностью вычисленные параметризованные части стеков (т.е. в них нет вызовов функций), соответствующих пути вычисления из корня грозди в данный лист грозди. Вершины грозди прогонки, обозначенные точками, являются реальными точками ветвления, а не только удобной формой представления в грозди. Причины, по которым параметризованное состояние вычислительной системы не показано в вершинах-точках, будут рассмотрены в одной из последующих заметок. Стартовая параметризованная конфигурация, задача на суперкомпиляцию, являющаяся корнем метадерева возможных вычислений, выделена указанием на неё стрелки-ребра, в исходящей вершине которого нет никакой конфигурации. Ребра грозди прогонки Г помечены предикатами выбора/расщепления конкретных значений параметров (выбора конкретного шага Рефал машины в момент исполнения преобразуемой программы).

Входными аргументами суперкомпилятора SCP4 здесь были нижеследующая Рефал программа p и указанная в корне Г задача на специализацию программы p (т.е. <Fab #e.x>). В данном примере в постановке задачи нет никакой заданной информации, по которой можно было бы содержательно проспециализировать программу p.

Fab { 
  'a' e.y = 'b' <Fab e.y>;
  s.x e.y = s.x  <Fab e.y>;
          = ; 
}

Приставки #, обозначающие параметры, на изображении не показаны, чтобы не загромождать его; такое решение не приводит к неоднозначности понимания картинки, так как гроздь прогонки всегда определена только в терминах параметров. Параметры являются семантическими объектами, а переменные программы p - синтаксическими объектами.

Отметим, что, в отличие от интерпретации конкретного (не параметризованного) стека вызова функций, разложение синтаксической композиции вызовов функций в стек, линейную последовательность их исполнения, может быть нетривиальным и зависит от стратегии суперкомпиляции. Примерами таких стратегий могут быть "ленивое" (call by need) и аппликативное (call by value) вычисление в процессе суперкомпиляции.

Для получения следующей пары картинок необходимо отдать команду в командной строке на консоли Рефал-5 интерпретатора.

Рисунок №3 показывает результаты первого и второго шагов трассировщика - левый и правый экраны соответственно. Результатом второго графического шага суперкомпилятора SCP4 является развитие дерева возможных вычислений задачи на суперкомпиляцию (пары - преобразуемой программы и ее параметризованной входной точки): результат второго вызова алгоритма прогонки был подклеен вместо листа левой ветви грозди прогонки, построенной предыдущим вызовом прогонки.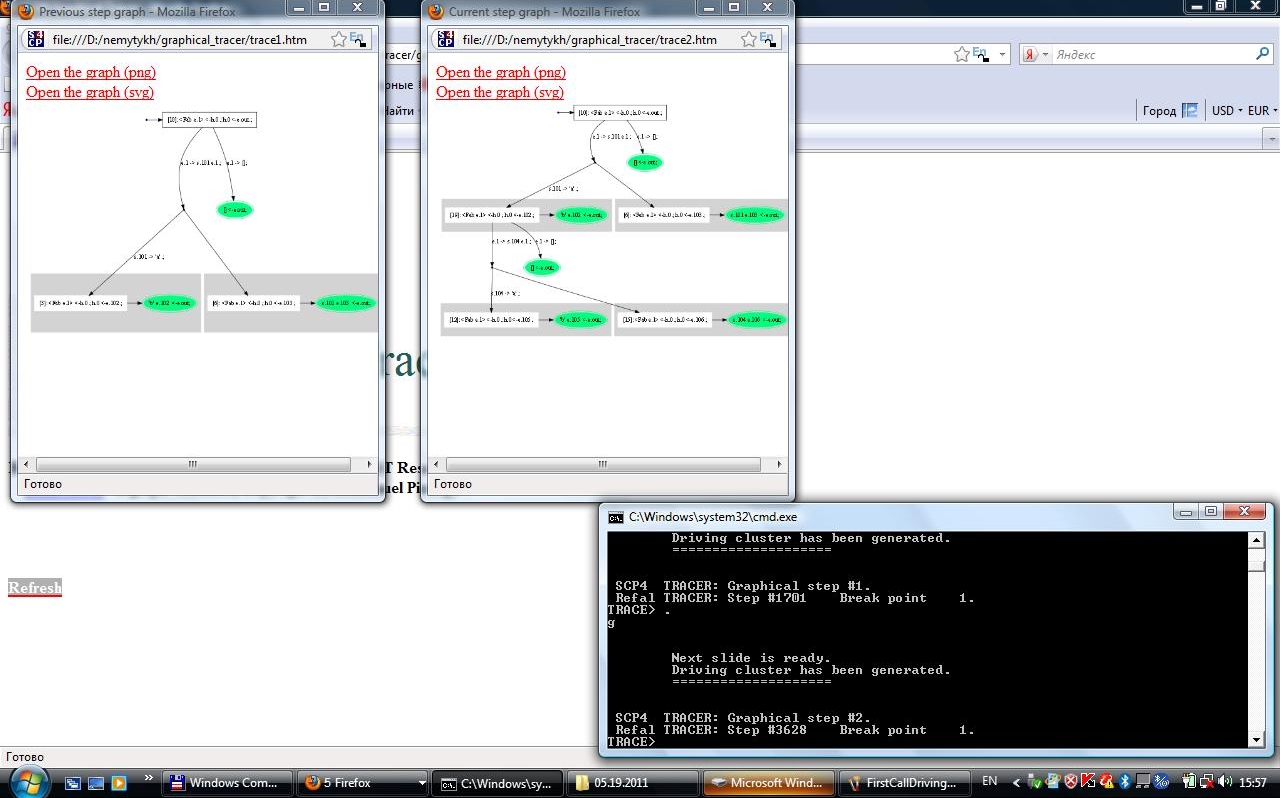

Рисунок 3. Результаты первого и второго вызовов прогонки.

В данной заметке мы вынуждены были обходить молчанием некоторые свойства грозди, построенной алгоритмом прогонки. Например, мы никак не пояснили: в чем заключается смысл выделения вершин-точек? Это и некоторые другие свойства грозди связаны с другими инструментами суперкомпиляции, которые используют данные свойства. Мы надеемся рассмотреть их в последующих заметках.

Мы закончили предыдущую заметку примером двухшагового развития дерева возможных вычислений задачи на специализацию <Fab #e.x>.

В том случае когда задача на специализацию Z программы p вырождается в задачу на исполнение (в постановке задачи нет параметров - она полностью определяется конкретными данными рассматриваемого языка программирования L), все шаги вычисления (интерпретации) входной точки (задачи Z) программы p полностью определены. Результат n-ого шага интерпретации STEPn (см. предыдущую заметку) однозначно определяет выбор веток "условных операторов" интерпретации шага STEPn+1. Если вычисление заканчивается за конечное число шагов N, тогда результат вычисления задачи Z есть результат шага STEPN: значение конфигурации, описывающей постановку задачи Z, или аварийная остановка. В этом случае мы имеем конечную последовательность шагов вычисления

STEP1,..., STEPN

Если p не завершается на входных данных, указанных в постановке задачи Z, тогда процесс вычисления представляется бесконечной последовательностью шагов:

STEP1,..., STEPn, …

Рассмотрим мета-аналог tree_dev (от tree developer) этого процесса вычислений. Как и при обычной интерпретации, мы будем допускать, что tree_dev может строить потенциально бесконечную структуру данных, не завершая своей работы за конечное время.

В случае общего положения, когда задача на специализацию Z параметризована, выбор веток "условных операторов" процесса вычисления может зависеть от неизвестных (но фиксированных) значений параметров.

Ниже мы будем рассматривать только корневые ориентированные деревья (далее кор-дерево), вершины и листы которых помечены параметризованными конфигурациями (параметризованными состояниями стека вызовов функций специализируемых программ - см. предыдущие заметки). Пусть V(T), L(T) обозначают соответственно множества вершин и листьев кор-дерева T.

Пусть даны два кор-дерева K, M. Скажем, что кор-дерево K накрывает кор-дерево M, если:

1. корень кор-дерева K совпадает с корнем кор-дерева M;

2. V(M) является подмножеством множества V(K);

3. L(M) является подмножеством L(K);

4. и любой путь v1, …, vk в кор-дереве M (здесь vi из V(M)) является подпоследовательностью некоторого пути в кор-дереве K.

"В первом приближении" алгоритм tree_dev можно понимать нижеследующим образом. tree_dev строит кор-дерево T, возможно бесконечное, которое накрывает кор-дерево SZ всех семантически возможных вычислений программы p, начинающихся из конфигурации постановки задачи Z, и которое накрывается кор-деревом ПZ всех синтаксически возможных процессов вычислений программы p, исходящих из той же параметризованной входной точки.

Содержательно кор-дерево SZ суть абстрактная операционная семантика программы p в контексте задачи Z, а кор-дерево ПZ является полной формальной синтаксической разверткой программы p. (Каждая программа представляет собой ориентированный граф с выделенной вершиной - точкой входа; этот граф можно формально развернуть в ориентированное дерево с корнем в точке входа.) При этом, абстрактная операционная семантика (как и формальная синтаксическая развертка) может зависеть от стратегий развёртки и может не совпадать с операционной семантикой конкретной модели вычислений в рассматриваемом языке программирования L. Мы требуем только одно: она должна сохранять значение программы p на области определения p.

Следующее пояснение понятия полной синтаксической развертки одновременно показывает некоторый набор возможных стратегий абстрактной операционной семантики и необходимость более сложных структур представления результатов этой развертки и алгоритма tree_dev, чем простого кор-дерева, данного в "первом приближении".

Рассмотрим два вложенных цикла на некотором псевдокоде. Пусть q и g некоторые предикаты, зависящие от состояния машины в точках их вычисления.

while (q)  { 
    A;            /* последовательность операторов */
    while (g) { 
    B;            /* последовательность операторов */
    }
    C;            /* последовательность операторов */
}
D;                /* последовательность операторов */

Рисунок 4. Фрагмент псевдокода программы.

В этом случае число итераций во время вычисления внешнего и внутреннего цикла зависит от входных данных программы и, следовательно, в общей ситуации не может быть известно во время преобразований (специализации) программы.

Если процесс синтаксической развертки данного фрагмента псевдокода следует естественному порядку работы этого псевдокода, тогда мы должны разворачивать внутренний цикл. Результат двух итераций такой развертки схематично показан ниже.

while (q) { 
    A;              
    if (g) then {
        B;                           
        if (g) then {
           B;                           
           while (g) { 
             B;                           
            }
        } else C;
    }
    else C;
}
D;

Рисунок 5. Результат двух итераций развертки первого типа.

И если предположить, что у нас есть магический инструмент бесконечной развертки, тогда внешний цикл будет разворачиваться только после построения внутреннего бесконечного дерева T. В процессе развертки внешнего цикла копии дерева T будут вставляться на ветки этой развертки.

Можно рассмотреть и другой порядок формальной развертки этих двух циклов: сначала разворачивается внешний цикл, а лишь затем копии внутреннего цикла. В этом случае схема результата двух итераций развертки будет выглядеть так:

 
if (q) then { 
    A;              
    while (g) { 
       B;                           
    }
    C;                             
    if (q) then { 
        A;              
        while (g) { 
           B;                           
        }
       C;                             
       while (q) {  
         A;              
         while (g) { 
            B;                           
         }
         C;                             
       }
    } else D;
} else D;

Рисунок 6. Результат двух итераций развертки второго типа.

Стратегии "ленивых" (call by need) вычислений в процессе суперкомпиляции соответствует некоторая комбинация приведенных выше разверток. Подробности будут рассмотрены нами в одной из последующих заметок.

Здесь мы только заметим, что осталось еще много неопределенности, которая должна быть устранена при разработке алгоритма tree_dev построения кор-дерева; например, в каком порядке разворачивать два первых цикла while (g) { … } (см. Рисунок 6). Мы временно абстрагируемся от этих неопределенностей и стратегий.

Прогонка суть основной инструмент развертки средствами суперкомпилятора - один шаг развертки. Корень будущего дерева развертки помечается задачей на специализацию Z - начальной параметризованной конфигурацией. Развертка начинается с корневой конфигурации: строится гроздь прогонки Г, далее прогоняется один из листьев (обозначим его a) грозди Г (точнее, - конфигурация, помечающая этот лист a). Лист a заменяется результатом его прогонки - гроздью Г_a, после чего следующий лист и т.д. Два шага этого процесса для реальных, не упрощенных конфигураций показаны на рисунках 2 и 3 (см. предыдущую заметку).

Таким образом, структура алгоритма развития дерева возможных вычислений программы p в контексте задачи на специализацию Z средствами суперкомпиляции выглядит следующим образом:

tree_dev(p,Z) {
  инициализация;
  while (построение кор-дерева развертки 
         в контексте задачи Z не завершено)
             { drv; }
  return (результирующее кор-дерево);
}

Где мы опустили аргументы прогонки drv. Алгоритм tree_dev является метарасширением интерпретатора (алгоритма интерпретации) языка L, на котором написана специализируемая программа p (см. заметку "О прогонке").

Int(p,d) {
  инициализация;
  while (вычисления не завершены)
             { STEP; }
  return (результирующее состояние);
}

Теперь мы готовы внести некоторые уточнения в данный выше набросок алгоритма tree_dev. Пусть дана программа p и задача на специализацию этой программы Z.

Для данной параметризованной конфигурации алгоритм прогонки drv строит гроздь Г, которая может содержать более одного листа с неполностью вычисленной конфигурацией (т.е. конфигурацией содержащей вызовы функций/подпрограмм программы p), помечающей этот лист. Ниже мы будем называть такие конфигурации/листы активными, а полностью вычисленные конфигурации/листы - пассивными. Ребра в грозди Г помечены предикатами, сужающими множества значений параметров и выбирающими конкретное вычисление. Ребра в Г также упорядочены согласно операционной семантике шага STEP, который проверяет (в этом порядке) логические ветвления (case, if).

На вход алгоритму tree_dev(p,rZ) подается лист rZ, помеченный конфигурацией постановки задачи Z.

Пусть дано дерево Tk с корнем rZ. Алгоритм tree_dev(p,Tk выбирает один из активных листов n дерева Tk и подаёт конфигурацию C, помечающую этот лист, на вход алгоритма drv(p,C).

Далее, если лист n не является корнем дерева Tk, тогда существует ребро (m,n). В этом случае Tk преобразуется в дерево Tk+1 следующим образом:
если результатом drv(p,n) является

• пустая гроздь, тогда ребро дерева (m,n) и лист n удаляются (ни одно из возможных вычислений, которое может начинаться с n, не заканчивается нормальной (неаварийной) остановкой с построением конкретного результата программы p на входных данных, указанных в постановке задачи на специализацию Z); пусть K - дерево, полученное в результате удаления ребра (m,n), - далее работает алгоритм if_transitive_node(K,m);

• непустая гроздь Г, тогда лист n заменяется на гроздь Г (т.е. корень rC грозди Г вставляется вместо листа n); пусть дерево K обозначает результат этой подстановки, - далее работает алгоритм if_transitive_node(K,rC).

Если лист n суть корень дерева Tk (т.е. оно состоит из одного листа), тогда Tk преобразуется в дерево Tk+1 следующим образом:
если результатом drv(p,n) является

• пустая гроздь, тогда дерево Tk+1 является пустым и алгоритм tree_dev(p,rZ) завершает работу;

• непустая гроздь Г, тогда строится ребро (n,rC), которое помечается всюду истинным предикатом (т.е. ничем); пусть дерево K обозначает результат этого преобразования, - далее работает алгоритм if_transitive_node(K,rC).

Пример двух последовательных деревьев развертки показан на Рисунке 3 из предыдущей заметки: слева дерево Tk, справа - дерево Tk+1.

На Рисунке 7 показан пример снимка экрана с изображением, построенным трассировщиком суперкомпилятора SCP4. Мы видим фрагмент дерева развёртки. Факт того, что результатом прогонки конфигурации является пустая гроздь, отмечен темной расцветкой листа, который помечает эта конфигурация. (Здесь мы не будем обращать внимание на странное ребро, входящее снизу в корень дерева. Изображение является трассировкой реального процесса суперкомпиляции и данное ребро появилось в результате работы механизмов, которые будут рассмотрены в последующих заметках.)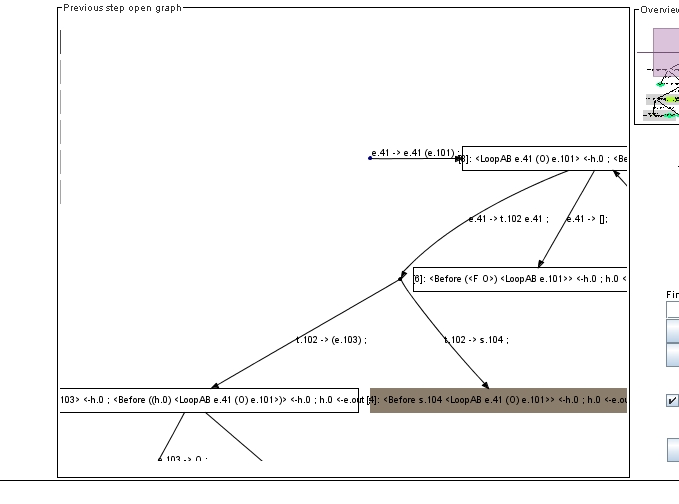

Рисунок 7. Фрагмент дерева развертки: в результате прогонки конфигурации, помечающей темный лист, получилась пустая гроздь.

На Рисунке 8 показан фрагмент того же дерева после удаления ребра, входящего в потемневший ("отсохший") лист. Из соображений компактности представления картинки трассировщик переставил ребра, исходящие из корня.

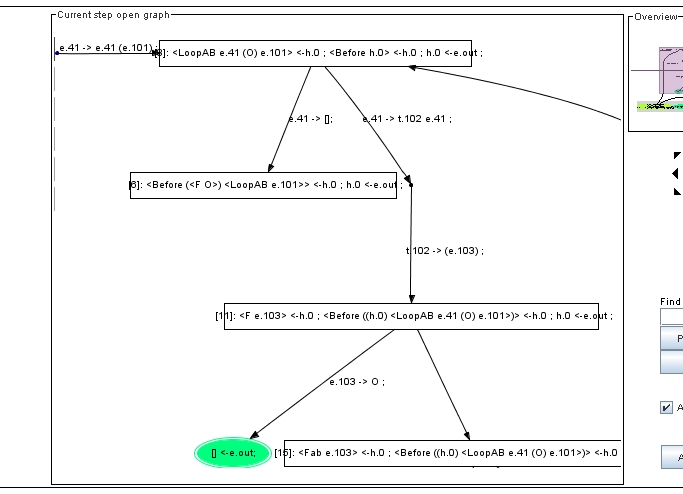
Рисунок 8. Фрагмент дерева развертки: в результате удаления ветви (см. Рисунок 7) появилась вершина с одним исходящим ребром.

Вершину (узел) в дереве T назовём транзитивной, если из неё выходит ровно одно ребро. Если вершина m дерева T является транзитивной, тогда алгоритм if_transitive_node(T,m): удаляет вершину m; преобразует ("склеивает") входящее в и выходящее из m рёбра в одно ребро, которое исходит из вершины, из которой исходило первое (входящее в m), и которое входит в вершину, в которое входило второе ребро; построенное ребро помечается композицией предикатов, которые помечали удаленные рёбра.

Рисунок 9 демонстрирует результат удаления транзитивной вершины, показанной на Рисунке 8. Входящее и исходящее в эту вершину ребра склеены в одно ребро, которое помечено предикатом, являющимся композицией предикатов, помечавших склеенные ребра. Из соображений компактности картинки трассировщик снова переставил ребра, исходящие из корня дерева развёртки: теперь их порядок совпадает с порядком на Рисунке 7.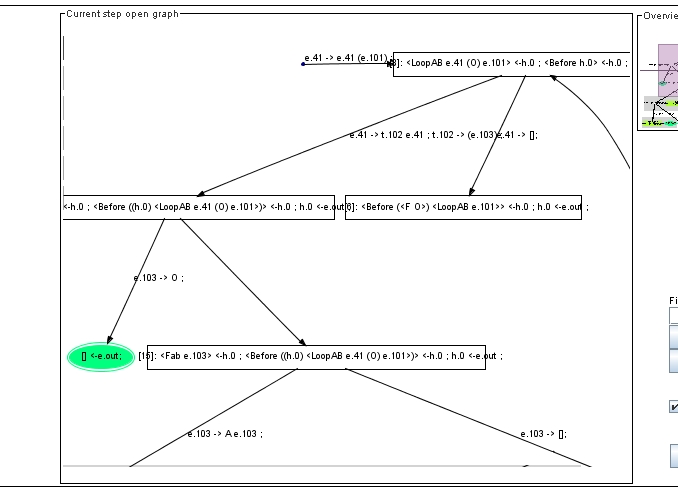

Рисунок 9. Фрагмент дерева развертки: удалена вершина с одним исходящим ребром (см. Рисунок 8), входящее и исходящее в эту вершину ребра склеены в одно ребро.

С абстрактной точки зрения, переход во время интерпретации программы p от одной конфигурации C1 (состояния) к другой конфигурации C2 требует действий построения C2. Следовательно, корректное удаление параметризованной конфигурации, описание которой включает в себя конкретную конфигурацию C2, из дерева развёртки программы p ведёт к ненужности выполнения этих действий в момент интерпретации. Абстрактное дерево развёртки является прототипом графа, представляющего программу - результат суперкомпиляции программы p. (Далее в наших заметках мы будем результат специализации называть остаточной программой.) Т.е. произошла оптимизация программы p: остаточная программа будет работать быстрее, - если на её вход подать данные, во время интерпретации обеспечивающие "прохождение" машины через ребро b, которое построил алгоритм if_transitive_node(T,m). Под "прохождением" через ребро мы имеем ввиду: попадание машины в одно из конкретных состояний, которые описываются параметризованной конфигурацией, из которой исходит ребро b, и положительный результат проверки условия, описанного предикатом на ребре b. Эта оптимизация произошла в контексте постановки задачи на специализации Z, которую решал суперкомпилятор.

С практической точки зрения, ситуация выглядит сложнее. Мы надеемся подробнее обсудить этот вопрос в одной из последующих заметок. Данную заметку мы завершим указанием на то, что алгоритм if_transitive_node(T,m) запускается только тогда, когда выбранная стратегия суперкомпиляции разрешает удаление транзитивных вершин.

В общем положении дерево (всех) возможных вычислений (см. предыдущую заметку) программы, преобразуемой суперкомпилятором в контексте данной задачи на специализацию, является бесконечным. Бесконечный процесс построения этого дерева не всегда оказывается бессмысленным, - также как бывают осмысленными программы незавершающие своей работы до физического выключения вычислительной машины (например: операционная система, коммуникационный протокол и т.д.). Однако, только в том случае когда процесс суперкомпиляции завершается и остаточная программа обладает какими-то содержательными свойствами оптимальности, которыми не обладает исходная, преобразуемая программа, мы можем говорить о результате суперкомпиляции. Требования завершаемости работы специализатора на всех входных программах и оптимальности полученных в результате таких завершений остаточных программ в общем случае являются противоречивыми. (В этой заметке мы никак не уточняем понятие "оптимальности" и обращаемся к интуиции читателя.) Это утверждение следует из алгоритмической неразрешимости задачи распознавания любого нетривиального семантического свойства программ, написанных на алгоритмически полных языках программирования (см. классическую теорему Успенского-Райса в монографии Н. К. Верещагина А. Шеня "Вычислимые функции." или здесь).

Бесконечное (точнее - не являющееся равномерно ограниченным по значениям входных параметров) дерево возможных вычислений T можно попытаться представить конечным графом. Процесс свертки дерева T в конечный граф является ключевым алгоритмом суперкомпилятора. По сути, только этим алгоритмом и отличаются разные суперкомпиляторы - от игрушечных-модельных до экспериментального. (Мы здесь говорим не о способе кодирования/программе, а именно об алгоритме.) В любом более-менее содержательном "суперкомпиляторе" этот алгоритм является очень сложным. Наиболее трудоемкий его под-алгоритм называется обобщением; к нему мы надеемся обратиться в наших последующих заметках - сначала описывая схематично и далее шаг за шагом вводя уточнения.

Будем смотреть на процесс свертки дерева T как на попытку доказательства следующего утверждения:

"Пусть дана программа p и задача на специализацию этой программы Z. Тогда дерево возможных вычислений T, соответствующее паре (p,Z), можно за конечное время свернуть (представить в виде) в некоторый конечный граф."

Конечно, здесь нужно уточнение. Что мы имеем в виду в выражении "представить в виде"? Необходимые пояснения будут даны ниже; на содержательном же уровне сформулированное выше утверждение, очевидно, имеет место, ибо дерево T получено в результате развёртки графа программы p в контексте задачи Z (см. заметку "О развитии дерева возможных вычислений"). Именно, например, в этот граф и можно свернуть дерево T. Могут, конечно, существовать (и всегда существуют!) и другие графы свёртки дерева T. И нас интересуют графы обладающие (в каком-то смысле) наилучшими свойствами оптимальности. Тонкий вопрос об оптимальности результата свёртки мы пока оставим за скобками рассмотрения. Мы встанем на точку зрения алгоритма свёртки, которому a priori вообще неизвестен ни один граф свёртки дерева T. Однако, мы будем предполагать, что поставленная задача построения графа свёртки может быть алгоритмически решена за конечное время посредством механизмов, о которых мы говорим ниже.

Рассмотрим первый модельный пример. Пусть множество данных в модельном языке программирования совпадает с множеством натуральных чисел. Проекцию на второй аргумент в этом языке можно неэффективно определить, например, так:

F(0,m) = m;
F(n+1,m) = F(n,m);

Рисунок 10. Программа q проекции на второй аргумент, написанная на модельном языке программирования.

Рассмотрим следующую задачу на специализацию: F(#n,#m). Построим дерево (всех) возможных вычислений пары (q, F(#n,#m)):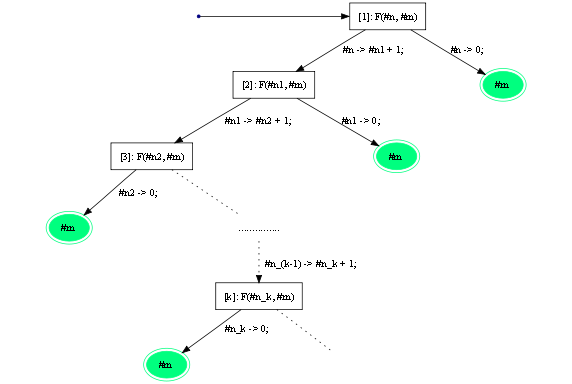

Рисунок 11. Дерево всех возможных вычислений
для (q, F(#n,#m)).

Здесь для компактности представления ветви на нижней части дерева переставлены местами. Ребра помечены предикатами на значения параметров. Предикат #n -> #j + 1 читается как "значение параметра #n имеет вид #j + 1", где справа и слева стоят разные параметры.

Наша цель - провести конструктивное доказательство возможности свертки этого бесконечного дерева в конечный граф. Будем регулярно обходить и анализировать это дерево от корня в глубину.

Ветвь, ведущая из корня дерева в зелёную вершину, соответствует значению параметра #n = 0. Эта ветвь конечна - зелёная вершина является листом. Следовательно, подграф, висящий на этой ветви, конечен и состоит из одного узла.

Второе ребро, исходящее из корня, сводит решение задачи специализации F(#n,#m) программы q к задаче специализации F(#n1,#m) той же самой программы q. Поскольку описание этих двух задач отличаются лишь именами параметров, то дерево развертки (дерево всех возможных вычислений) первой задачи совпадает с точности до имён параметров с деревом развёртки второй задачи. Следовательно, решение второй задачи можно свести к решению первой задачи посредством замены значения параметра #n на значение параметра #n1:
#n := #n1;. Или то же самое на языке графов: можно с точностью до переименования параметров отождествить вершину [2] с вершиной [1] и таким образом свернуть ветвь развёртки задачи F(#n,#m), соответствующую предикату

#n -> #n1+1;,

в конечный граф. (Если бы не было оговорки "с точностью до переименования", тогда подобное отождествление в математике называется факторизацией.) Результат описанной свёртки представлен на рисунке 12, в котором оставлена информация о замене/подстановке параметров, позволившей свернуть основную ветвь дерева развёртки.

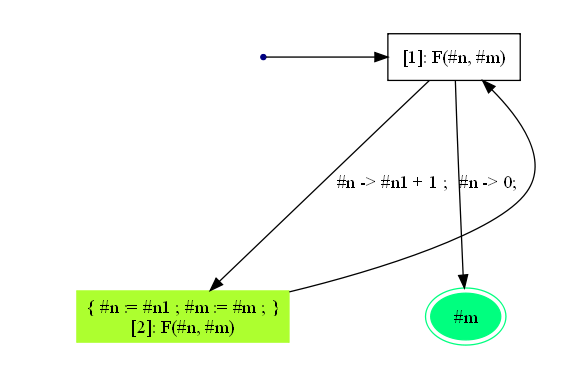
Рисунок 12. Граф - результат свёртки дерева всех возможных вычислений задачи (q, F(#n,#m)).

Отметим, что подстановка, сводящая вычисления, которые могут начаться из одной вершины дерева развёртки, к вычислениям, которые могут начаться из другой вершины, может иметь более сложную структуру, чем в разобранном выше примере.

Например, для программы вычисления суммы первого и второго аргумента:

F(0,m) = m;
F(n+1,m) = F(n,m+1);

Рисунок 13. Программа вычисления суммы её входных аргументов.

Результат свёртки дерева возможных вычислений задачи на специализацию F(#n,#m) будет отличаться от графа на рисунке 12 только подстановкой сведения: она в этом случае будет иметь следующий вид #n := #n1; #m := #m+1;.

Подобным образом - с помощью замены параметров - сводить одну задачу специализации Z2 некоторой программы p к другой задаче специализации Z1 этой же программы можно и тогда, когда множество возможных вычислений, начинающихся в задаче Z2, является подмножеством множества возможных вычислений, начинающихся в задаче Z1, а необязательно совпадает с ним. Важно только чтобы задача Z1 в процессе свёртки дерева возможных вычислений T уже рассматривалась раньше задачи Z2 - здесь происходит шаг математической индукции по построению дерева T. При этом в T может не существовать пути из вершины, в которой описана Z1, в вершину, в которой описана Z2. Такой путь существует в рассмотренном выше модельном примере.

Напомним, что задача на специализацию описывается посредством параметризованной конфигурации (см. Заметку 2).

Если одну параметризованную конфигурацию C2 в дереве T можно свести посредством подстановки параметров σ можно свести к другой параметризованной конфигурации C1 в T, тогда говорят, что конфигурация C2 вкладывается в конфигурацию C1 посредством σ.

При рассмотрении конкретной вершины v в дереве T может существовать несколько ранее рассмотренных вершин u1, …., un, в параметризованные конфигурации из которых C1, …., Cn, вкладывается конфигурация Cv, помечающая вершину v. Следовательно, возникает необходимость в стратегии выбора одной конфигурации из множества C1, …., Cn, к которой и будет сведена конфигурация Cv. Мы откладываем вопрос обсуждения таких стратегий на последующие заметки.

Внимательный читатель уже отметил, что обсуждаемое в этой заметке понятие вложения одной конфигурации в другую ему также (как и понятие прогонки) давно известно из школьного курса математики. Это замена переменных при решении алгебраических уравнений. При этом уравнение играет роль конфигурации, а переменные роль параметров. Смысл замены переменных состоит в том, чтобы свести процесс решения одного уравнения к решению другого уравнения, которое ученик уже умеет решать. Например, методом замены переменных биквадратные уравнения от одной переменной сводятся к квадратным уравнениям от другой переменной. При этом школьник должен запомнить саму замену переменных, чтобы, решив получившееся квадратное уравнение, можно было найти корни исходного биквадратного уравнения. По аналогичной причине мы оставляем в графе свёртки информацию о подстановках сведения одной конфигурации к другой (см. Рисунок 12).

Пусть дано дерево развертки T некоторой задачи на специализацию (q, Z). Всегда ли существуют две разные вершины v, u дерева T такие, что либо конфигурация Cu вкладывается в конфигурацию Cv, либо конфигурация Cv вкладывается в конфигурацию Cu? От ответа на этот вопрос зависит необходимость каких-то других, дополнительных механизмов для свёртки дерева T в конечный граф или можно обойтись описанным выше приемом вложения одной вершины в другую.

Ответ на поставленный вопрос отрицательный. Построим соответствующий пример. Рассмотрим программу q, данную на рисунке 13. Дерево возможных вычислений задачи на специализацию F(#n,1) этой программы показано на рисунке 14.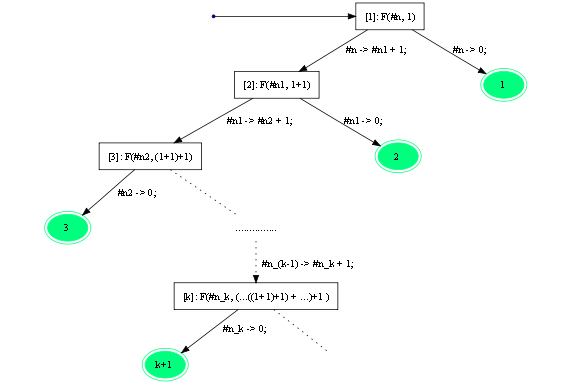

Рисунок 14. Дерево всех возможных вычислений для
(q, F(#n,1)).

Вторые аргументы всех конфигураций из вершин ветвления этого дерева являются константами и все эти константы различны. Следовательно, ни одна из конфигураций не может быть вложена в другую.

Таким образом, чтобы свернуть произвольное дерево развёртки в конечный граф, необходимы дополнительные инструменты, которые мы надеемся обсудить в наших последующих заметках.

Данное выше неформальное описание процесса свёртки принимает на вход всё дерево возможных вычислений T программы p в контексте выбранной задачи на специализацию Z. Как правило, T является бесконечным. Нашим объектным языком программирования является рефал, множество данных которого суть множество конечных последовательностей произвольных конечных деревьев. Следовательно, все алгоритмы суперкомпиляции могут работать только с элементами последовательности конечных деревьев

T1, T2, …, Tn, ….,

которые аппроксимируют/приближают дерево возможных вычислений T. Зафиксируем некоторое число k и рассмотрим дерево Tk. Предположим, что мы свернули одну из потенциально бесконечных ветвей дерева Tk. Дерево Tk превратилось в граф Gk - в этом графе имеется цикл (см. Рисунок 12). Начиная с этого момента входные структуры данных для большинства алгоритмов суперкомпиляции логически становятся, в общем случае, графами, а не деревьями. (Именно логически, поскольку эти графы кодируются в рефале деревьями.) И, строго говоря, при необходимости последующего развития Gk - развёртки по другим веткам дерева Tk, на которых алгоритм свёртки еще не работал, мы будем получать вместо рассмотренной выше последовательности деревьев последовательность конечных графов

T1, T2, …, Gk, ….,Gn, ….,

которые также, в некотором смысле, приближают дерево возможных вычислений T (если заново развернуть их свёрнутые ветви).

Иногда мы будем называть графы Gk, ….,Gn частично свёрнутыми деревьями, таким образом подчёркивая, что в этих графах есть выделенная вершина - корень дерева Tk (мы будем называть эту вершину корнем графа) и (потенциально) бесконечные пути - несвёрнутые ветви дерева Tk.

Пусть v некоторая вершина частично свёрнутого дерева Tk. Обозначим через reduce(Tk, v) некоторый алгоритм попытки свёртки пути из корня частично свёрнутого дерева Tk, содержащего вершину v. Вызов алгоритма reduce(Tk, v) пытается вложить конфигурацию Cv в одну из конфигураций, из некоторого подмножества S вершин wj, уже рассмотренных предыдущими вызовами этого же алгоритма reduce(Ti, wj), где i < k.

Попытка вложения может оказаться:

• неудачной - конфигурация Cv не вкладывается ни в одну из конфигураций Cw_j, где wj пробегает множество S;

• либо удачной - в множестве S нашлась вершина wm такая, что Cv вкладывается в Cw_m; и в этом случае ветвь, содержащая вершину v, сворачивается в цикл.

Наша ближайшая цель - выписать первое приближение структуры алгоритма суперкомпиляции. Ранее (см. Заметки 2, 3) мы подчёркивали, что алгоритмы прогонки и развития дерева возможных вычислений являются метарасширениями алгоритмов интерпретатора объектного языка программирования (в нашем случае - рефала). Для алгоритма вложения нет соответствующего подалгоритма интерпретатора, для которого вложение можно было бы рассматривать как его метарасширение. Некоторую аналогию с вложением можно было бы указать в мемоизирующем интерпретаторе (интерпретаторы рефала таковыми не являются), который следит за множеством всех вызов функций, которые уже полностью вычислены к моменту очередного вызова F(x0,…,y0), и сохраняет значения этих предыдущих вызовов в таблице мемоизации. Следовательно, такому интерпретатору нет необходимости заново вычислять значение F(x0,…,y0) - оно уже известно - нужно просто его скопировать из таблицы. В данном случае имеет место вложение (посредством тождественной подстановки) вызова F(x0,…,y0) в один из вызовов, который уже встречался в истории вычислений задачи, данной интерпретатору.

При построении первого приближения структуры алгоритма суперкомпиляции SCP мы будем отталкиваться от структуры алгоритма развития дерева возможных вычислений программы p в контексте задачи на специализацию Z (см. Заметку "О развитии дерева возможный вычислений"). Напомним его, явно выписав аргумент прогонки:

tree_dev(p,Z) {
   инициализация;
   while (построение кор-дерева развертки
          в контексте задачи Z не завершено)
              { v := один из листов кор-дерева;
                drv(Cv);
              }
   return (результирующее кор-дерево);
}


Здесь, как и выше по тексту, Cv обозначает параметризованную конфигурацию, помечающую лист v.

Теперь мы явно укажем последовательность приближений к результирующему кор-дереву. Получим:

tree_dev(p,Z) {
   T1 := вершину, помеченную описанием задачи Z;
   i := 1;
   while (построение кор-дерева развертки
          в контексте задачи Z не завершено)
              { v := один из листов кор-дерева Ti;
                cluster := drv(Cv);
                T(i+1) := заменить в Ti лист v гроздью
                         прогонки cluster;
                i := i+1;
              }
   return (результирующее кор-дерево);
}


Где корень грозди прогонки вставляется вместо листа v.

Первое приближение структуры алгоритма суперкомпиляции:

SCP(p,Z) {
   T1 := вершину, помеченную описанием задачи Z;
   i := 1;
   while (в Ti несвёрнутый (потенциально)
          бесконечный путь)
              { v := один из листов кор-дерева Ti;
                cluster := drv(Cv);
                T(i+1) := заменить в Ti лист v гроздью
                         прогонки cluster;
                i := i+1;
                if (в cluster существует
                    нетранзитивная вершина)
                  {   v := первую от корня
                           нетранзитивную вершину
                           грозди прогонки cluster;
                      reduce(Ti, v);
                  };
              }
   return (результирующий граф);
}


Сделаем несколько замечаний:

• Алгоритм вложения reduce(Ti, v) пытается вложить не конфигурацию Cv из листа v дерева, а конфигурацию из первой вершины ветвления грозди, полученной в результате прогонки конфигурации Cv, если такая вершина существует. Прогонка конфигурации Cv позволяет определить некоторые свойства Cv - с точки зрения оптимизации частично свёрнутого дерева Ti+1. Например, если конфигурация Cv является транзитивной и может быть вложена в одну из конфигураций из множества S (см. выше), тогда свёртка, выполненная перед прогонкой, ветви, на которой находится лист v, оставит необходимость исполнения программой - результатом суперкомпиляции действий преобразования конфигурации Cv (после подстановки конкретных значений параметров этой конфигурации), которые можно было бы выполнить во время суперкомпиляции - равномерно по значениям параметров. Вызов алгоритма прогонки нужен здесь, чтобы определить является конфигурация Cv транзитивной или не является.

• С другой стороны, игнорирование транзитивных вершин в процессе свёртки может привести к незавершаемости работы суперкомпилятора; и решение об оформлении циклов из вершин, помеченных транзитивными конфигурациям, должно приниматься одной из стратегий, что не отражено в данной нами выше схеме алгоритма суперкомпиляции.

• В структуре алгоритма SCP также явно не указаны стратегии выбора: (1) листа v частично свёрнутого дерева, конфигурация Cv из которого будет прогоняться; (2) конкретной конфигурации из множества S (см. выше), в том случае если в S существует несколько конфигураций, в которые может быть вложена Cv; (3) выбор самого множества конфигураций S.

Проследим работу описанной выше структуры алгоритма суперкомпиляции на примере специализации аналога программы, данной на рисунке 10, в контексте соответствующей задачи на специализацию в терминах языка рефал. Трасса построена графическим трассировщиком суперкомпилятора SCP4. В частности, дадим некоторые пояснения по языку описания трассы, который мы будем использовать в наших заметках. Ниже дано определение соответствующей программы.

F { 
          (e.m)  = e.m;
  e.n '1' (e.m)  = <F (e.n) (e.m)>;
}

Рисунок 15. Программа q проекции на второй аргумент, написанная на языке программирования рефал.

Задача на специализацию, соответствующая рисунку 11, в терминах рефала определяется так: <F #n (#m)>. На выходе прогонки этой стартовой конфигурации имеем нижеследующую гроздь.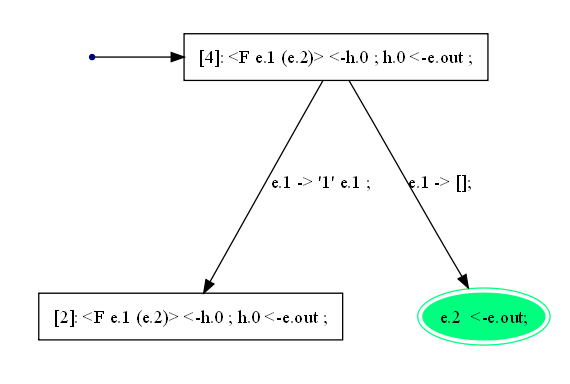

Рисунок 16. Гроздь результата прогонки конфигурации
<F #n (#m)>,
описывающей задачу на специализацию программы q.

Эта гроздь прогонки совпадает с деревом T2. По техническим причинам суперкомпилятор SCP4 переименовал/заменил параметры. Безымянное ребро выходит из служебной вершины, в которой записана подстановка #n := e.1; #m := e.2; - произошедшая замена параметров. Эта подстановка не показана на рисунке и нужна для корректного описания входной точки остаточной программы. Напомним (см. "О прогонке"), что в трассе параметры не помечаются приставкой #. Кроме конфигураций, как мы понимали их выше, вершины грозди содержат дополнительные записи. Мы объясним их тогда, когда будем разбирать примеры, где эти записи по существу; в данном примере на них можно не обращать внимания. Одна из вершин (листов) прогонки окрашена. Зелёный цвет указывает на то, что конфигурация, помечающая эту вершину, не требует дальнейших преобразований. В данном случае она пассивна - не содержит вызовов функций. Правая ветвь помечена предикатом e.1 -> [];: здесь знак [] используется для обозначения пустого выражения (пустой последовательности). Описание предиката на левой ветви является сокращением следующего определения:

"e.1 -> '1' e.x, где e.x новый уникальный параметр,
и e.1 := e.x;".

То есть значения одноименных параметров e.1 справа и слева от знака "->" являются разными. В наших заметках начиная с этого места, если не оговорено обратное, мы будем придерживаться соглашения, что значения всех параметров слева от знака сужения "->" не совпадает со значениями одноимённых параметров справа от знака сужения.

В дереве T2 нет ни одной активной вершины, расположенной выше вершины [4], конфигурация из которой была подана на вход прогонки: множество S вершин, в которые можно было бы пытаться вложить конфигурацию <F e.1 (e.2)>, является пустым множеством. Согласно структуре алгоритма SCP выбираем лист дерева T2. Это дерево имеет единственный активный лист. Подаём конфигурацию, помечающую этот лист, на вход очередного вызова алгоритма прогонки. На рисунке 17 показано дерево T3.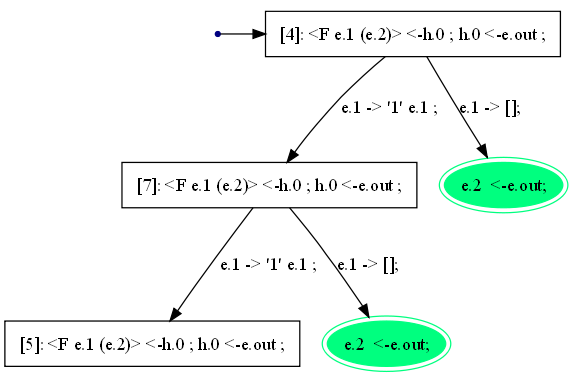

Рисунок 17. Дерево T3.

На рисунке 18 трассировщик синим цветом показал вершину v дерева T3, которая подается на вход алгоритма reduce(T3, v).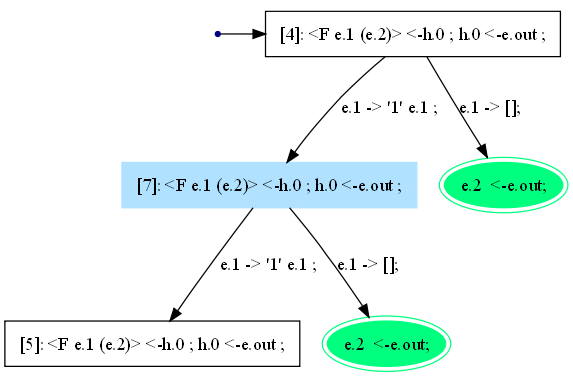

Рисунок 18. Дерево T3: синим цветом показан второй аргумент вызова reduce(T3, v).

В данном случае суперкомпилятор SCP4 выбирает в качестве множества S множество всех вершин, принадлежащих пути из коня T3 в вершину v. Множество S содержит единственную вершину. На рисунке 19 эта вершина показана желтым цветом.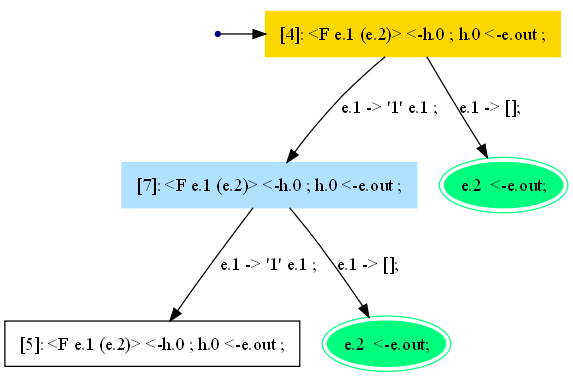

Рисунок 19. Дерево T3: попытка вложения конфигурации из синей вершины в конфигурацию из жёлтой вершины.

Конфигурация из вершины v вкладывается в конфигурацию, помечающую корень, посредством тождественной подстановки. Дерево возможных вычислений полностью свёрнуто в конечный граф (см. Рисунок 20).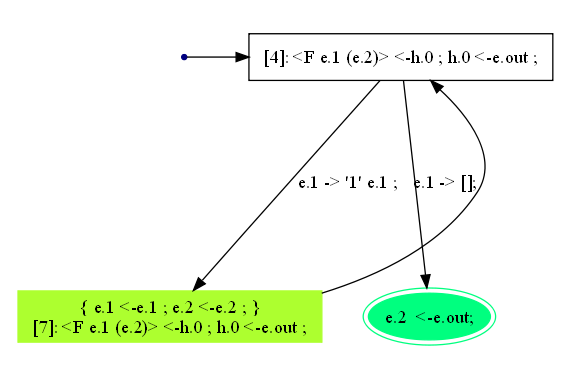

Рисунок 20. Конечный граф, представляющий свёртку дерева возможных вычислений для (q, <F #n (#m)>).

Активная вершина 3, 4 Активная конфигурация 3 Активный лист 3, 4 Вложение конфигурации 4 Гроздь прогонки 2, 3, 4 Дерево возможных вычислений 2, 3, 4 Задача на специализацию 1, 2, 3, 4 Задача на суперкомпиляцию 2 Конфигурация 2, 3, 4 Кор-дерево 3, 4 Корень графа 4 Корневое дерево 3

Обобщение конфигураций Остаточная программа 3, 4 Параметризованная конфигурация 2, 3, 4 Пассивная вершина Пассивная конфигурация 3, 4 Пассивный лист 3 Прогонка 2, 3, 4 Сужение параметра 4 Транзитивная вершина 3, 4 Частично свёрнутое дерево 4

drv 3, 4 reduce 4 SCP 4 tree_dev 3, 4 -> 4 <- []