Материалы занятий
- Числа Фибоначчи. 2 октября, 2016 г.
Упорядоченный набор чисел (или символов) называется последовательностью. Элементы последовательности удобно помечать их порядковыми номерами, которые записываются как нижние индексы.
Рассмотрим нижеследующую последовательность Фибоначчи:
$1, \ \ \; 1, \ \ 2, \ \ 3, \ \ \, 5, \ \ 8, \ldots$
$F_1, F_2, F_3, F_4, F_5, F_6, \ldots$
Два первых элемента этой последовательности равны $F_1 = F_2 = 1$, а каждый последующий равен сумме двух предыдущих: если $n > 2$, то $F_n = F_{n-1} + F_{n-2}$.
Эта последовательность, названная в честь итальянского математика Леонардо Пизанского сына Боначчо, обладает интересными свойствами и встречается в совершенно удивительных явлениях природы.
Элементы этой последовательности называются числами Фибоначчи.
Начнем с названия. «Сын Боначчо» переводится на итальянский язык как «filius Bonacci». Отсюда возникло сокращение «fi-Bonacci» - отчество Леонардо Пизанского, а буква «c» в итальянском языке читается как русская «ч».
Простейшие свойства чисел Фибоначчи:
(1) Сумма первых $n$ чисел Фибоначчи равна:$F_1 + F_2 + \ldots + F_n = F_{n+2} -1$
(2) Сумма чисел Фибоначчи с нечетными номерами:$F_1 + F_3 + F_5 + \ldots + F_{2n-1} = F_{2n}$
(3) Сумма чисел Фибоначчи с четными номерами:$F_2 + F_4 + \ldots + F_{2n} = F_{2n+1} - 1$
(4) Паркет из квадратов $F_i \times F_i$:Для каждого числа Фибоначчи $F_i$ вырежем по одному квадрату $K_i$, длина стороны которого равна $F_i$. Такими квадратами можно замостить плоскость - выложить паркет - без дырок и наложений квадратов, используя все квадраты. Сделать это можно разными способами.
На картинке показано начало замощения одним из таких способов:
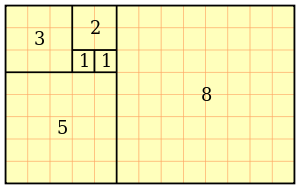
Начало замощения плоскости квадратами
$K_1, K_2, K_3, K_4, K_5, K_6$Следующий квадрат $K_7$ нужно приложить сверху, $K_8$ - слева и т.д., двигаясь по часовой стрелке. Ниже показан другой способ замещения - по часовой стрелке:

Числа Фибоначчи встречаются в живой и неживой Природе:
Семечки на подсолнухе образуют два семейства спиралей. Спирали одного семейства раскручиваются по часовой стрелке, другого - против часовой стрелки. На разных подсолнухах число спиралей в одном семействе может быть разным, что кажется естественным.
Но вот что поражает воображение: какой бы подсолнух мы не выбрали, число спиралей в одном семействе (например, - по часовой стрелке) равно некоторому числу Фибоначчи!

На этом подсолнухе $F_9 = 34$ спирали,
накрученные по часовой стрелке и $F_{10} = 55$
спирали - против часовой стрелки.Чешуйки на сосновой шишке тоже образуют два семейства спиралей. Считать эти спирали уже сложнее, но их число тоже совпадет с одним из чисел Фибоначчи!

Сколько спиралей каждого семейства на этой шишке?Соединив плавной линией расположенные по диагонали углы квадратов, которыми мы замостили плоскость, снова получим спираль:
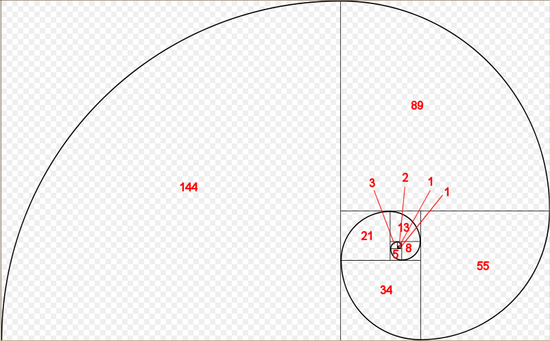
Спираль Архимеда.Именно по этой спирали закручена раковина улитки:

Улитка.Галактика, в которую входит наша солнечная система, также закручена по этой спирали. Другие примеры использования чисел Фибоначчи Природой можно посмотреть, например, здесь или здесь.
- Числа Фибоначчи (продолжение). 9 октября, 2016 г.
Картинки (см. материалы к предыдущему занятию), демонстрирующие замощение плоскости квадратами со сторонами, длины которых равны числам Фибоначчи, доказывают следующее свойство этих чисел:
(4) Сумма квадратов первых $n$ чисел Фибоначчи равна:$F_1^2 + F_2^2 + \ldots + F_n^2 = F_n \times F_{n+1}$
Игра в классики.На асфальте мелом нарисована слева направо прямая полоса, разделенная на $n$ одинаковых прямоугольных клеток. Девочка встает на первую (самую левую) клетку. За один ход она может выбрать одно из трёх действий:
(1) остаться на месте;
(2) прыгнуть на соседнюю клетку вправо;
(3) прыгнуть через одну клетку вправо.
Клетки большие, поэтому она не может перепрыгнуть через две клетки. Прыгать разрешается только вперёд - слева направо.Сколько существует разных способов попасть в последнюю, $n$-ю, клетку? Два способа движения называются разными, если множество клеток, в которых побывала девочка, прыгая первым способом, не совпадает с аналогичным множеством при движении вторым способом.
Если $n > 2$, тогда, чтобы попасть в $n$-ю клетку, нужно либо побывать во второй клетке, либо перепрыгнуть через вторую клетку. Любой путь, проходящий через вторую клетку, отличается от пути, который через эту клетку не проходит (т.е. в этом случае девочка перепрыгнула через вторую клетку). Попасть во вторую клетку можно единственным способом. Также существует только один способ перепрыгнуть вторую клетку, который сразу ведет в третью клетку.
Значит общее число путей из первой клетки в $n$-ю клетку равно число путей из второй клетки в $n$-ую клетку плюс число путей из третьей клетки в $n$-ую клетку.
Обозначим число путей, про которые спрашивается в исходной задаче, через $x_n$. Тогда число путей из второй клетки в в $n$-ую клетку равно $x_{n-1}$, так как вторая клетка на одну клетку ближе к $n$-ой клетке. Если бы мы начинали считать со второй клетки, то $n$-ая клетка получила бы $(n-1)$-й номер. Аналогично получаем, что число путей из третьей клетки в $n$-ю клетку равно $x_{n-2}$.
Выше мы уже заметили, что множество первых путей не пересекается с множеством вторых путей. Следовательно, получаем $x_n = x_{n-1} + x_{n-2}$.
Эта формула не дает ответа на вопрос, сколько путей ведёт из первой клетки в первую клетку и сколько путей ведёт из первой клетки во вторую клетку. Поскольку девочке разрешается за один ход вообще никуда не сдвигаться, то $x_1 = 1$. Нетрудно понять, что $x_2$ тоже равно $1$: $x_2 =1$.
Следовательно, искомое число путей равно $n$-ому числу Фибоначчи: $x_n = F_n$. Задача решена. $\Box$
Задача
Рассмотрим сеть путей, изображенную на рисунке ниже. Сколько существует путей, которыми можно, двигаясь вдоль стрелок, переехать:
(1) из вершины $A$ в вершину $C_n$,
(2) из вершины $B$ в вершину $C_n$?
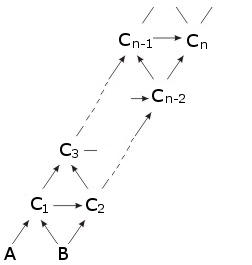
Сеть железнодорожных путей. - Фибоначчиева система счисления. 16 октября, 2016 г.
Числа создал Господь Бог. Они существуют сами по себе - независимо от нас.
Различные системы счисления являются разными способами представления чисел на бумаге и доске.
Обычно используется арабская позиционная система счисления; возможно, с разными основаниями (десятичная, двоичная и т.д.). Иногда используется римская система счисления.
Числа Фибоначчи дают еще один способ взаимно-однозначного представления целых чисел посредством некоторого подмножества конечных последовательностей нулей и единиц.
Рассмотрим произвольное положительное число $A$. Представим его как сумму наибольшего числа Фибоначчи $F_n$, не превосходящего $A$, и некоторого неотрицательного числа $B_1$: $A = F_n + B_1$, где $F_n \leq A$ и целое число $B_1 \ge 0$.
По определению, $F_1 = F_2 = 1$, а все остальные числа Фибоначчи попарно различны и больше $1$. Следовательно, указанное выше число $F_n$ всегда единственно, за исключением случая, когда оно равно $1$. В этом случае выберем большее по номеру: $F_2$.
Теперь число $B_1$ можно аналогичным способом разложить в сумму $B_1 = F_k + B_2$. То же самое можно сделать для $B_2$ и т.д. При этом для всех $i$ $B_i > B_{i+1}$ (почему?). Cреди чисел Фибоначчи есть $1$. Следовательно, через некоторое конечное число шагов $m$ число $B_m$ будет равно $0$.
Описанный выше процесс однозначно представляет число $A$ в виде конечной суммы
различных чисел Фибоначчи. Действительно, каждое следующее число Фибоначчи, входящее в эту сумму, определяется только соответствующим ему числом $B_i$. Слагаемые этой суммы упорядочены по убыванию слева направо.Полученную сумму, в свою очередь, можно представить как строку из единиц и нулей длины $n$, начинающуюся с $1$. Эта лидирующая единица соответствует первому слагаемому $F_n$ (см. выше). Далее на $i$-ом месте ($i < n$) ставим $1$, если число $F_i$ входит в разложение, иначе ставим $0$.
Например, $19 = 13 + 6 = 13 + 5 + 1 = F_7 + F_5 + F_2$. Поэтому $19$ представляем строкой $1010010$. Из $F_1 = F_2 = 1$ следует, что в разложении
любого числа последний символ-цифра будет $0$ (почему?). Поэтому последний ноль в разложении целого положительного числа писать не будем.Окончательно получаем Фибоначчиево представление числа $19 = 101001_{f}$, где мы приписали к строке индекс $f$, чтобы отличать её от представления числа в двоичной системе счисления.
Теорема 1: Для любого целого числа $A$ его Фибоначчиево представление не содержит двух подряд идущих единиц.
Теорема 2: Любая строка из нулей и единиц, которая начинается с $1$ и не содержит двух подряд идущих единиц, является Фибоначчиевым представлением некоторого целого положительного числа.
- Системы счисления и способы короткой записи последовательностей чисел в алфавите из двух символов.
23 октября, 2016 г.Мы уже знаем, что запись числа в двоичной системе счисления будет короче, чем в Фибоначчиевой, поскольку во втором случае не все последовательности нулей и единиц представляют собой запись числа. А именно, последовательность, содержащая две единицы подряд, не является записью числа в Фибоначчиевой системе счисления. Попробуем использовать это свойство Фибоначчиевой системы.
Компания SpeedLine изменила тариф на пересылку сообщений на Марс. Теперь она берет не $100\$ $ за знак (который может быть лишь $0$ или $1$), а $500\$ $ за первый знак и по $50\$ $ за все следующие. Саша хочет научиться передавать Даниилу два числа от $1$ до $200$ за как можно меньшую плату. У Саши и Даниила есть возможность заранее условиться, в какой именно форме будут передаваться числа. Как Саше следует действовать?
Любое натуральное число, не превышающее $200$, будет иметь не больше $8$ разрядов в двоичной системе счисления и не больше $11$ разрядов в Фибоначчиевой (почему?). Пересылать такие короткие числа разными сообщениями по новому тарифу очень не выгодно. Значит, нужно придумать способ записать их в одном сообщении так, чтобы получатель мог однозначно отделить одно число от другого. Просто записать две последовательности друг за другом - не решение: например, сообщение $1001010$ Даниил может понять и как передачу пары $100$ и $1010$, и как передачу пары $10010$ и $10$. Рассмотрим три разных подхода к решению задачи.
1) Избыточная двоичная запись. Будем записывать числа в двоичной системе счисления (как самой экономичной), но каждый разряд удваивать, а в качестве разделителя возьмем пару разных символов (например, пару $01$). Например, двоичная запись $101011$ в таком случае превратится в $110011001111$. Разбив полученное сообщение на пары последовательных символов, Даниил сразу же найдёт среди этих пар $01$ и поймёт, что это разделитель, значит, слева от него стоит первое число, а справа - второе. Такое решение дает возможность Саше передать в худшем случае $34$ знака.
2) Фибоначчиева запись. Будем записывать числа в Фибоначчиевой системе счисления, а разделителем объявить последовательность $11$. Такая последовательность не может встретиться внутри числа, значит, она всегда будет стоять на стыке между двумя разными числами. При этом за ней заведомо стоит $1$ (поскольку второе число не меньше $1$, а значит, его Фибоначчиева запись начинается с $1$), а после этой $1$ - либо конец сообщения (если второе число равно $1$), либо $0$. Отыскав в полученном сообщении последовательность, состояющую минимум из трёх единиц подряд, Даниил сразу же может понять, что две предпоследние единицы в этой последовательности - разделитель. Слева от него стоит первое число, справа - второе. Такое решение позволяет Саше обойтись в худшем случае $24$ знаками.
3) Двоичная запись и длинный разделитель. Будем записывать числа в двоичной системе счисления безо всяких ухищрений, но придумаем хитрый разделитель, который бы позволил Даниилу однозначно установить, где кончается двоичная запись первого числа и где начинается двоичная запись второго. На первый взгляд кажется, что это невозможно. Однако мы знаем, что числа, которые предлагается передавать, не могут быть больше $200$. Поэтому назначим разделителем последовательность из восьми нулей: она не может принадлежать никакому числу до $200$, к тому же после нее заведомо идет единица (первый разряд второго числа). Такое решение тоже позволяет Саше обойтись в худшем случае $24$ знаками.
Оказывается, что какое бы решение ни выбрал Саша, он может так изменить разделитель, чтобы сэкономить $50\$ $ (ещё один знак), а в первом случае можно придумать такой способ представления двоичных единиц и нулей, чтобы переплачивать вдвое лишь за один тип знака (например, удваивать лишь $1$, оставляя нули одиночными). Но даже после этого изменения первый способ передачи сообщений остается самым невыгодным. И хотя суммы, которые Саше придётся выложить за передачу самого дорогого сообщения способами $2$ и $3$, совпадут, в среднем ему выгоднее пользоваться способом $2$, чтобы не переплачивать за длинный разделитель между короткими числами.
Попробуйте понять, какими из способов 1-3 можно пользоваться, чтобы передавать в одном сообщении сколько угодно чисел от $0$ до $200$?
Какой длины нужно брать разделитель, чтобы способ 3 работал на числах от $1$ до $N$?
- Системы счисления и способы короткой записи последовательностей чисел в алфавите из двух символов (продолжение). 30 октября, 2016 г.
На предыдущем занятии мы рассмотрели свойства двух способов записи положительных чисел для пересылки двоичных сообщений. А именно:
А) запись чисел в Фибоначчиевой системе счисления с разделителем из одной единицы;
Б) запись чисел в двоичной системе счисления с длинным разделителем.Если Саше придется посылать на Марс два числа не из множества от $1$ до $200$, а из множества от $1$ до $M$, то длина разделителя в способе Б будет в худшем случае равна длине числа $M$ в двоичной системе счисления. Следовательно, если нужно переслать два двоичных числа, каждое из которых записывается $K$ знаками, то при использовании способа Б потребуется $3K$ цифр.
Утверждение 1: Наибольшее число длины $K$ в Фибоначчиевой системе есть $F_{K+2}-1$.
И способ А, и способ Б записи чисел требуют тем больше знаков, чем больше записываемое число. Значит, больше всего денег Саше придется заплатить, если ему требуется переслать два одинаковых числа $M$ (самых больших среди множества тех, которые можно пересылать).
При пересылке двух чисел, записанных в Фибоначчиевой системе с помощью $K$ знаков каждое, придется заплатить за $2K+1$ знака. За эту же цену способом с длинным разделителем можно переслать два числа длины $[\frac{2K+1}{3}]$ каждое, где $[x]$ - ближайшее целое число, не превосходящее $x$. Самое большое число, которое можно записать с помощью $[\frac{2K+1}{3}]$ знаков, используя двоичную систему счисления, есть число из $[\frac{2K+1}{3}]$ единиц. Оно равно $2^{[\frac{2K+1}{3}]+1}-1$, или, что то же самое, $2^{[\frac{2K+1}{3}]} \times 2-1$. Если оно больше, чем $(K+2)$-е Фибоначчиево число, значит, в худшем случае способ записи Б будет дешевле способа записи А. И наоборот, если оно меньше, чем $(K+2)$-е Фибоначчиево число, значит, в худшем случае способ записи A будет дешевле способа записи Б. Поэтому нам нужно сравнить $(K+2)$-е число Фибоначчи и число $2^{[\frac{2K+1}{3}]} \times 2$.
Сложность в том, что мы не знаем, как посчитать $N$-ое число Фибоначчи, кроме как из соотношения $F_{N+1} = F_N + F_{N-1}$. В частности, мы не знаем, можно ли выразить их как степени некоторого числа $\Phi$, умноженные на некоторое число $\alpha$, так что $\Phi^1\times\alpha = F_1$, $\Phi^2\times\alpha = F_2$ и вообще $\Phi^K\times\alpha = F_K$. Если бы это было возможно, то дробь $\frac{F_{N+1}}{F_N}$ была бы равна $\Phi$ для любого $N$. Однако числа $\frac{3}{2}$, $\frac{5}{3}$, $\frac{8}{5}$, $\frac{13}{8}$ (и так далее) все различны.
Попробуем вычислить разность $\frac{F_{N+1}}{F_N} - \frac{F_N}{F_{N-1}}$.
Утверждение 2: Разность $\frac{F_{N+1}}{F_N} - \frac{F_N}{F_{N-1}}$ равна $\frac{1}{F_N \times F_{N-1}}$, если $N$ нечетно, и $\frac{-1}{F_N \times F_{N-1}}$, если $N$ четно. Более кратко: $\frac{F_{N+1}}{F_N} - \frac{F_N}{F_{N-1}} = \frac{(-1)^{N+1}}{F_N \times F_{N-1}}$.
Доказательство.
Для нескольких первых чисел это утверждение можно проверить прямым вычислением.Дальше предположим, что формула
$\frac{F_{N+1}}{F_N} - \frac{F_N}{F_{N-1}} = \frac{(-1)^{N+1}}{F_N \times F_{N-1}}$ выполняется для всех $N \leq N_1$.Тогда $F_{N_1+1}F_{N_1-1} - F_{N_1}^2 = (-1)^{N_1+1}$.
По определению чисел Фибоначчи $F_{N_1-1} = F_{N_1+1}-F_{N_1}$. Подставим это выражение в формулу выше. Получим:
$F_{N_1+1}F_{N_1+1}-F_{N_1+1} \times F_{N_1} - F_{N_1}^2 = (-1)^{N_1+1}$,
$F^2_{N_1+1}-F_{N_1}\times(F_{N_1+1} + F_{N_1}) = (-1)^{N_1+1}$,
$F^2_{N_1+1}-F_{N_1} \times F_{N_1+2} = (-1)^{N_1+1}$,
$F_{N_1} \times F_{N_1+2} - F^2_{N_1+1} = (-1)^{N_1+1}\times(-1)$,
$\frac{F_{(N_1+1)+1}}{F_{N_1+1}} - \frac{F_{N_1+1}}{F_{N_1}} = (-1)^{(N_1+1)+1}$Положим $N_2 = N_1+1$. Последнее равенство показывает, что наша формула выполняется и для $N_2$.
Теперь мы знаем, что наша формула выполняется для всех $N \leq N_2$, и можем применить это же рассуждение, заменив $N_1$ на $N_2$, чтобы доказать ее для $N_2+1$. Таким образом можно поступать, чтобы вывести ее для любого $N_1+L$. Значит, формула $\frac{F_{N+1}}{F_N} - \frac{F_N}{F_{N-1}} = \frac{(-1)^{N+1}}{F_N \times F_{N-1}}$ выполняется для всех $N$. Утверждение доказано. $\Box$
Числа, равные разностям между $\frac{F_N}{F_{N-1}}$ и $\frac{F_{N+1}}{F_{N}}$ - это дроби с числителем $1$ или $-1$ и знаменателем, большим, чем $F_{N-1}^2$. Такие дроби с ростом $N$ очень скоро становятся близки к $0$. Значит, где-то далеко в последовательности чисел Фибоначчи разница $\frac{F_N}{F_{N-1}} - \frac{F_{N+1}}{F_{N}}$ станет очень малой, и если обозначить $\frac{F_{N}}{F_{N-1}}$ как $\Psi$, то $F_{N+1}$ будет примерно равно $F_{N}\times\Psi$. Посчитав $\Psi$ для нескольких первых чисел Фибоначчи, мы увидим, что $\Psi$ близко к ${1.6}$. Можно показать, что c ростом $N$ $\Psi$ будет все ближе и ближе к $\Phi = \frac{1+\sqrt{5}}{2}$. Эта пропорция называется золотым сечением и была известна ещё в античности. Замечательна она, в частности, тем, что $1-\Phi$ = $\frac{1}{\Phi}$.
Хотя мы доказали, что каждое следующее число Фибоначчи больше предыдущего примерно в $\Phi$ раз, это ещё не полное доказательство того, что мы можем приблизить $K$-ое число Фибоначчи числом вида $\Phi^K\times\alpha$. Выполнено следующее утверждение, доказательства которому мы не даем.
Утверждение 3: Положим $\alpha = \frac{1}{\sqrt{5}}$. Число $\Phi^K\times\alpha$, округленное до целого, есть $K$-ое число Фибоначчи.
- Системы счисления и способы короткой записи последовательностей чисел в алфавите из двух символов (часть III). 6 ноября, 2016 г.
Сравнение двух чисел, записанных в виде степеней, - не всегда легкая задача. Скажем, трудно сразу ответить на вопрос, что больше: $A_1 = \frac{2^{100}}{\sqrt{2}}$ или $A_2 = \frac{3^{80}}{\sqrt{3}}$? Напомним следующее свойство возведения в степень двух положительных чисел.
Предложение. Пусть $a>0$, $b>0$, $N$ - натуральное число. Тогда из $a^N > b^N$ следует $a>b$, и наоборот.
Возведем оба сравниваемых выражения в квадрат, получим $A_1^2 = \frac{{(2^5)}^{20}}{2}$, $A_2^2 = \frac{{(3^4)}^{20}}{3}$, или, что то же самое, $A_1^2 = 16\times{(2^5)}^{19}$, $A_2 = 27\times{(3^4)}^{19}$. Теперь уже ясно, что $A_1^2 < A_2^2$, значит, и $A_1 < A_2$.
Вернемся к нашим расчётам с компанией межпланетной мобильной связи SpeedLine (см. материалы предыдущего занятия).
Пусть в нашем распоряжении есть сумма, достаточная, чтобы заплатить SpeedLine за пересылку $K$ двоичных цифр. Продолжим изучать вопрос, какие два наибольших числа $X$ одинаковой длины можно передать на Марс за эти деньги, если мы пользуемся методом записи в системе Фибоначчи (кратко - методом А) и методом записи в двоичной системе с длинным разделителем (кратко - методом Б).
Длина разделителя в методе А равна единице, а все остальные знаки делятся поровну между двумя числами. Поэтому передать можно максимум два числа размером $\frac{[K-1]}{2}$, то есть два фибоначчиевых числа с $\frac{[K-1]}{2}+2$-ым номером минус $1$. Используя метод записи в двоичной системе с длинным разделителем, мы должны потратить на разделитель столько же знаков, сколько содержит передаваемое число наибольшей возможной разрядности. Так что на запись одного числа остается всего $[\frac{K}{3}]$ знаков - и максимальное число, которое мы можем с помощью них записать, есть $2^{[\frac{K}{3}]}-1$.
Что же больше: $F_{\frac{[K-1]}{2}+2}$ или $2^{[\frac{K}{3}]}$?
Для первых нескольких $K$ мы можем узнать ответ, подсчитав эти два числа. В частности, для $K=9$ $F_6 = 2^3$ и способы записи А и Б равноценны. Для $K=15$ уже $F_9 = 34$, $2^5 = 32$, и способ А выигрышнее. Для $K=16$ можно передать также, самое большее, два числа $F_9-1$ или же $2^5-1$, и опять выигрывает способ А. Однако если $K=18$, то способом А можно передать максимум $54$ знаков, а способом Б - $63$. Связано это с тем, что $18$ делится на $3$, но $18 - 1$ не делится на $2$, и способом А приходится пересылать числа на одину цифру короче. Однако уже для такого же числа $K = 36$ имеем $F_{19} > 2^{12}$. Аналогично способ А оказывается экономичней и для $K = 31,32,33,34,35$.
Можно ли показать, что способ А выигрышнее, чем Б, и для больших $K$?
Мы уже знаем, что для некоторых $K_1$ (а именно, от $31$ до $36$ включительно) способом A можно передать, самое большее, два числа $L_1-1$, где $L_1 = F_{\frac{[K_1-1]}{2}+2}$, а способом Б - два числа $L_2-1$, где $L_2 = 2^{[\frac{K}{3}]}$, причем $L_1>L_2$. Рассмотрим, что можно передать за $K_2 = K_1+6$ знаков.
Способом А: два числа Фибоначчи, с номером, на $3$ большим, чем номер числа $L_1$, уменьшенных на $1$, то есть $F_{[K_1-1]/2+2+3}-1$.
Из Утверждения 2 (см. предыдущее занятие) можно вывести, что все следующие разности $\frac{F_{[(K_1-1)/2]+2+1}}{F_{[(K_1-1)/2]+2}}-\frac{\sqrt{5}+1}{2}$, $\frac{F_{[(K_1-1)/2]+2+2}}{F_{[(K_1-1)/2]+2+1}}-\frac{\sqrt{5}+1}{2}$, $\frac{F_{[(K_1-1)/2]+2+3}}{F_{[(K_1-1)/2]+2+2}}-\frac{\sqrt{5}+1}{2}$ не больше по модулю, чем $\frac{1}{F_{[(K_1-1)/2]+2}*F_{[(K_1-1)/2]+1}}$. Значит, $F_{[(K_1-1)/2]+2+3}$ отличается от $(\frac{\sqrt{5}+1}{2})^3 \times F_{[(K_1-1)/2]+2}$ не больше, чем на $\frac{F_{[(K_1-1)/2]+4}\times(\Phi^2+\Phi+1)}{F_{[(K_1-1)/2]+2} \times F_{[(K_1-1)/2]+1}}$, где $\Phi = \frac{\sqrt{5}+1}{2}$. Уже для $K_1=19$ $\frac{F_{[(K_1-1)/2]+4}\times(\Phi^2+\Phi+1)}{F_{[(K_1-1)/2]+2} \times F_{[(K_1-1)/2]+1}} = \frac{(\Phi^2+\Phi+1) \times 233}{55 \times 89} < \frac{1}{2}$, а уж тем более это неравенство выполнено для $K_1\geq 31$. Поэтому $F_{[(K_1-1)/2]+2+3}$ есть $(\frac{\sqrt{5}+1}{2})^3 \times L_1$, округленное до целого. И способом А за $K_2$ знаков можно передать два числа $(\frac{\sqrt{5}+1}{2})^3 \times L_1-1$, округленных до целых.
Способом Б: два числа вида $2^{[\frac{K_1+6}{3}]}-1$, что есть $2^{[\frac{K_1}{3}]}\times 2^{2}-1$.
Теперь, если мы установим, что ${(\frac{\sqrt{5}+1}{2})}^3> 2^2$, то этим докажем, что за $K_2$ знаков способом А действительно можно передать числа больше, чем способом Б.
${(\frac{\sqrt{5}+1}{2})}^3 = \frac{5\sqrt{5}+3\times (\sqrt{5})^2+3\times\sqrt{5}+1}{8} = \sqrt{5}+2$. Поскольку $\sqrt{5}>2$, эта сумма больше $4$, и требуемое неравенство доказано.
Итак, мы установили, что если способ А выгоднее, чем способ Б, когда мы ограничены $K_1$ знаками, то он выгоднее и для $K_1+6$ знаков, а значит, и для $K_1+ {6 \times T}$ знаков при любом натуральном $T$. К тому же есть шесть идущих подряд случаев $31$ - $36$, когда способ А выгоднее, чем способ Б. Возьмём любое число $M$, большее $31$. Какое-нибудь из чисел $31$ - $36$ (назовем его $M_0$) будет давать такой же остаток при делении на $6$, что и $M$, так что $M = M_0 + {6 \times T}$. Это доказывает, что и для ограничения в $M$ знаков способ А будет выгоднее, чем Б. $\Box$
Задача.
Опишем следующий способ В пересылки двух чисел. Оба числа сначала переводим в троичную систему счисления, а затем заменяем полученные троичные цифры по правилу:
$0$ заменяем на пару $00$,
$1$ заменяем на пару $01$,
$2$ заменяем на пару $10$,
а разделитель записывается как $11$.Например, $100$ в троичной системе счисления есть $10201$, $50$ - $1212$. Передача $100$, а затем $50$ будет осуществляться в способе В строкой $01001000011101100110$. Получатель, разделив эту строку на пары символов, однозначно восстановит числа, которые в ней зашифрованы.
Пусть мы можем заплатить за передачу только $K$ знаков. Удастся ли способом В передать с их помощью большие числа, чем способами А или Б?
- Арифметика в системе счисления Фибоначчи. Сложение.
13 ноября, 2016 г.Пусть мы выбрали некоторую систему счисления. Тогда нам нужно придумать способы выполнения обычных арифметических действий над числами, записанными в этой системе счисления.
Таких способов существует много.
Внешние способы.
Например, бывают косвенные способы выполнения арифметических действий. Саша выучил алгоритмы основных арифметических действий с числами, представленными в десятичной системе счисления. Они для него стали очень привычными. Это еще не означает, что он хорошо понимает эти алгоритмы! Ему рассказали про другую систему счисления, алгоритмы арифметических действий в которой достаточно сильно отличаются от алгоритмов в десятичной системе. Саша, в силу привычки (или лени), предпочитает сначала перевести числа из непривычной системы счисления в десятичную. Далее произвести с ними требуемое действие в десятичной системе. После чего результаты этого действия записать в новой системе счисления.Внутренние способы.
Предположим, однако, что Сашу с самого начала обучали арифметике в системе счисления, отличной от десятичной. Тогда Саша не смог бы воспользоваться косвенным способом выполнения арифметических действий, поскольку он не знает никакой системы счисления, кроме той, которую ему только что рассказали. В этом случае возможность лениться будет ограничена.Будем интересоваться внутренними способами выполнения арифметических действий над числами, записанными в системе счисления Фибоначчи. При этом было бы странным предварительно стереть все свои существующие знания. Поэтому иногда для объяснений мы будем использовать и понятия десятичной системы счисления, чтобы сделать изложение более кратким. Десятичная система также полезна для проверки наших вычислений.
Сложение столбиком.
Пусть даны два числа в системе счисления Фибоначчи: $A = \overline{a_{n} \ldots a_2}_f = a_{n} \times F_{n} + \ldots + a_2 \times F_2$, $B = \overline{b_{m} \ldots b_2}_f = b_{m} \times F_{m} + \ldots + b_2 \times F_2$, где $F_i$ - $i$-ое число Фибоначчи, $a_n = b_m = 1$ и $n \ge m > 1$.
Требуется вычислить
$\overline{a_n \ldots a_m \ldots a_k \ldots a_2}_f$ $+$ $\overline{b_m \ldots b_k \ldots b_2}_f$ В промежуточных вычислениях будем представлять числа $A$ и $B$ в виде сумм чисел Фибоначчи, но эти представления не обязательно будут представлениями в системе счисления Фибоначчи. Номера чисел Фибоначчи в этих суммах не будут возрастать. Мы будем допускать: (1) несколько подряд идущих единиц - коэффициентов перед соответствующими последовательными числами Фибоначчи; (2) более того, - не более двух подряд идущих равных чисел Фибоначчи.
Например, может встретиться сумма
$F_7 + F_6 + F_5 + (F_3 + F_3) + F_2$ , но сумма$(F_7 + F_7) + F_6 + F_5 + (F_3 + F_3 + F_3) + F_2$ , встретиться не может.Такие суммы также будем кратко записывать в виде последовательностей. Например,
$11121_{*} = F_7 + F_6 + F_5 + (F_3 + F_3) + F_2$, где звездочка показывает, что строка является промежуточным представлением числа, а не представлением Фибоначчи.Алгоритм сложения в системе счисления Фибоначчи покажем на примере.
Пример:
${10101010}_f$ $+$ $\,{1001}_f$ В отличие от сложения в десятичной системе счисления, складывать будем начиная со старших разрядов - слева направо. После сложения цифр каждого разряда промежуточный результат будем записывать в первом слагаемом.
В результате сложения цифры старшего - четвертого разряда второго слагаемого с цифрой четвертого разряда первого слагаемого получим:
${10102010}_{*}$ $+$ $\;{001}_f$ Теперь преобразуем первое слагаемое в систему счисления Фибоначчи.
Заметим, что если $k > 2$, тогда
$2 \times F_k = F_k + F_k = F_k + (F_{k-1} + F_{k-2}) =$ То есть если $k > 2$, тогда $2 \times F_k = F_{k+1} + F_{k-2}$.
$ = (F_k + F_{k-1}) + F_{k-2} = F_{k+1} + F_{k-2}$.Это равенство показывает, что от двойки в четвертом разряде первого слагаемого можно избавиться посредством двух переносов: переноса $1$ на один разряд влево и переноса $1$ на два разряда вправо.
Поскольку перед сложением первое слагаемое было записано в системе счисления Фибоначчи, то разряд, перенесенный влево, сложится с $0$. Так будет всегда, когда мы складываем два числа, записанных в системе счисления Фибоначчи, поскольку в таком представлении не могут встретиться две подряд идущие единицы. При переносе $1$ вправо может появиться $2$, поскольку перенос перепрыгивает через разряд.
В нашем примере получаем:
${10110020}_{*}$ $+$ ${001}_f$ Теперь избавимся от двойки во втором разряде первого слагаемого. Сделать это аналогично двойке в четвертом разряде не удастся, так как в этом случае $k=3$ и мы можем использовать только один разряд справа.
Имеем:
$2 \times F_3 = F_3 + F_3 = F_3 + (F_2 + F_1) =$ То есть в этом случае нужны: перенос $1$ на один разряд влево и перенос $1$ на один разряд вправо.
$= (F_3 + F_2) + F_1 = (F_3 + F_2) + F_2 = F_4 + F_2$.После эти переносов получаем:
${10110101}_{*}$ $+$ $\,{001}_f$ Теперь нужно избавиться от двух идущих подряд единиц. $F_{k+1} = F_{k} + F_{k-1}$, поэтому две единицы переносятся как одна $1$ в соседний разряд слева от заменяемой пары. Саму пару единиц заменяем нулями.
${11000101}_{*}$ $+$ $\,{001}_f$ Аналогично избавляемся от двух единиц в старших разрядах, добавляя еще один разряд слева:
${100000101}_{f}$ $+$ $\;{001}_f$ Теперь первое слагаемое записано в системе счисления Фибоначчи. Поэтому можно продолжить сложение старшего разряда второго слагаемого с соответствующим ему разрядом первого слагаемого. Лидирующие нули второго слагаемого пропускаем.
Получаем:
${100000102}_{*}$ $+$ $\;{0}_f$ Второе слагаемое исчерпано - далее его писать не будем. Чтобы получить окончательный ответ, осталось преобразовать первое слагаемое в систему счисления Фибоначчи.
$2 \times F_2 = 2 = F_3$. То есть в этом случае нужен только один перенос $1$ на один разряд влево.
Получаем:
${100000110}_{*}$ Избавляемся от двух единиц, идущих подряд:
${100001000}_{f}$ Вычисление искомой суммы закончено. Осталось заметить, что во всех наших промежуточных вычислениях сумма двух слагаемых не менялась и, как мы знаем, каждая строка из нулей и единиц, которая не содержит подряд идущих единиц, представляет некоторое число в системе счисления Фибоначчи.
Ответ:
${10101010}_f$ $+$ ${1001}_f$ $\overline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }$ ${100001000}_{f}$ Вышеприведенный пример показывает все шаги и структуру алгоритма сложения в общем случае - для двух произвольных положительных целых чисел, записанных в системе счисления Фибоначчи:
(1) сложение по разрядам происходит слева направо;
(2) после сложения очередного разряда первое слагаемое переводится в систему счисления Фибоначчи;
(3) при этом переводе сначала убирается двойка, - сразу как только она появляется при сложении разрядов либо при предыдущих шагах преобразования в систему Фибоначчи; таким образом, в первом слагаемом никогда не могут возникнуть две «цифры» $2$;
(4) если первое слагаемое не содержит «цифры» $2$, тогда убираем подряд идущие единицы;
(5) действия с тремя младшими разрядами первого слагаемого отличаются от действий с остальными разрядами.Действия удаления двоек и двух подряд идущих единиц из промежуточных представлений первого слагаемого чередуются друг с другом. Возникает вопрос, не существует ли пара чисел, сложение которых приведенным выше алгоритмом попадет в «порочный» круг? Не повезло ли нам при выборе конкретной пары чисел, которую мы складывали?
Поставленный вопрос разрешается следующим образом. Каждое конкретное действие удаления двойки или пары единиц включает в себя перенос единицы в соседний старший разряд. С другой стороны, каждое промежуточное первое слагаемое меньше некоторого числа Фибоначчи. Другими словами, длина первого слагаемого, представленного в системе Фибоначчи, ограничена. Следовательно, число переносов в старшие разряды конечно, что прерывает предполагаемый «порочный» круг.
- Арифметика в системе счисления Фибоначчи.
Вычитание. Таблицы умножения. 20 ноября, 2016 г.Пусть даны два числа $A > B$ в системе счисления Фибоначчи: $A = \overline{a_{n} \ldots a_2}_f = a_{n} \times F_{n} + \ldots + a_2 \times F_2$, $B = \overline{b_{m} \ldots b_2}_f = b_{m} \times F_{m} + \ldots + b_2 \times F_2$, где $F_i$ - $i$-ое число Фибоначчи, $a_n = b_m = 1$ и $n \ge m > 1$.
Мы хотим вычислить разность
$\overline{a_n \ldots a_m \ldots a_k \ldots a_2}_f$ $-$ $\overline{b_m \ldots b_k \ldots b_2}_f$ В промежуточных вычислениях будем придерживаться соглашений, которые использовали в алгоритме сложения. Вычитать будем начиная со старших разрядов - слева направо. После вычитания цифр каждого разряда промежуточный результат будем записывать в уменьшаемом.
Как и для сложения, алгоритм покажем на конкретном примере.
Пример:
${100001000}_{f}$ $-$ $\,{10101010}_f$ Попытка вычитания старшего разряда вычитаемого числа приводит к неудаче: нужно занимать из старшего разряда уменьшаемого числа. На основании равенства $F_{i+2} = F_{i+1} + F_{i}$ уменьшаемое число можно написать в промежуточном представлении в виде:
${011001000}_{*}$ $-$ ${10101010}_f$ Теперь над старшим разрядом вычитаемого стоит $1$. Вычитаем эту единицу и опускаем лидирующие нули.
${1001000}_{f}$ $-$ ${101010}_f$ Снова занимаем из старшего разряда вычитаемого числа.
${0111000}_{*}$ $-$ ${101010}_f$ После вычитания старшего разряда получаем:
${11000}_{*}$ $-$ ${1010}_f$ Здесь мы не будем спешить переводить промежуточное представление уменьшаемого числа в систему Фибоначчи, иначе над старшим разрядом вычитаемого числа окажется ноль и мы снова вынуждены будем занимать.
${10000}_{f}$ $-$ ${10}_f$ Здесь приходится занимать не из соседнего разряда, а из более старшего. Получаем:
${1100}_{*}$ $-$ ${10}_f$ Теперь нужно занимать из единицы, полученной на предыдущем шаге.
${1011}_{*}$ $-$ ${10}_f$ Осталось сделать последнее вычитание.
${1001}_{f}$ $-$ ${0}_f$ Ответ:
${100001000}_{f}$ $-$ ${10101010}_f$ $\overline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }$ ${1001}_f$ Мы видим, что алгоритм вычитания в системе счисления Фибоначчи проще алгоритма сложения. В рассмотренном примере нам немного повезло: в общем случае вторая из двух единиц, которые возникают, когда занимаем из старших разрядов, может привести к промежуточной двойке:
${101}_{f}$ $-$ ${10}_f$ Здесь получаем:
${12}_{*}$ $-$ ${10}_f$ После вычитания получим:
${2}_{*}$ От двойки избавляемся так же, как и в алгоритме сложения, используя равенство $F_2 + F_2 = 2 = F_3$.
${2}_{*} = {10}_{f}$ Слишком рано от двойки избавляться тоже не стоит, как мы выше поступили с парой идущих подряд единиц.Таблицы умножения.
В десятичной системе счисления, как и в двоичной или троичной и т.п., очень просто умножать числа вида $\overline{a_n 0 0 \ldots 0}$ на цифру $b$, зная школьную таблицу умножения всех цифр, с ее помощью умножить $a_n$ на $b$ и к результату приписать нули.
В более сложном случае тоже легко расправляемся с нулями: $\overline{a_n a_{n-1} \ldots a_1 0 0 0} \times \overline{b_m b_{m-1} \ldots b_1 0 0} = $ $= \overline{c_k c_{k-1} \ldots c_1 0 0 0 0 0}$, где $\overline{c_k c_{k-1} \ldots c_1} = \overline{a_n a_{n-1} \ldots a_1} \times \overline{b_m b_{m-1} \ldots b_1}$
В системе счисления Фибоначчи цифры очень простые, но умножать на десятку, сотню, тысячу намного сложнее, чем в десятичной системе. Поэтому приходится составлять таблицы умножения на такие числа.
$F_3 = 10_{f}$ $F_4 = 100_{f} $ $F_5 = 1000_{f} $ $F_6 = 10000_{f} $ Нижеследующую таблицу умножения можно вычислить по определению умножения как суммы нескольких копий одного из сомножителей, например: $M \times F_4 = M + M + M $
Пусть $M = 100101_{f} = 17$, тогда начало таблицы для $M \times F_{i}$ выглядит так (проверьте!):
$M \times F_2$ $=$ $100101_{f}$ $=$ $17$ $M \times F_3$ $=$ $10000000_{f}$ $=$ $34$ $M \times F_4$ $=$ $10100101_{f}$ $=$ $51$ $M \times F_5$ $=$ $101010001_{f}$ $=$ $85$ $M \times F_6$ $=$ $1010100000_{f}$ $=$ $136$ - Арифметика в системе счисления Фибоначчи.
Умножение и деление. 27 ноября, 2016 г.На предыдущем занятии мы вычислили начало таблицы умножения для $M \times F_{i}$, где $M = 100101_{f} = 17$. Немного продолжим её:
$M \times F_2$ $=$ $100101_{f}$ $=$ $17$ $M \times F_3$ $=$ $10000000_{f}$ $=$ $34$ $M \times F_4$ $=$ $10100101_{f}$ $=$ $51$ $M \times F_5$ $=$ $101010001_{f}$ $=$ $85$ $M \times F_6$ $=$ $1010100000_{f}$ $=$ $136$ $M \times F_7$ $=$ $10101000001_{f}$ $=$ $221$ $M \times F_8$ $=$ $101010000001_{f}$ $=$ $357$ Задача.
Попробуйте угадать следующую строчку этой таблицы, а затем проверьте догадку с результатом прямого вычисления.Ниже мы будем пользоваться этой таблицей при демонстрации алгоритмов умножения и деления в системе счисления Фибоначчи.
Умножение.
Школьный алгоритм умножения столбиком в десятичной системе счисления основан на простом наблюдении. Если нам нужно вычислить, например, $65 \times 47$, тогда мы можем разбить второй сомножитель на два слагаемых, раскрыть скобки и вспомнить что приписывание к числу справа нуля соответствует умножению этого числа на десять:
$65 \times 47 = 65 \times (40 + 7) = 65 \times 40 + 65 \times 7 = $
$= (65 \times 4) \times 10 + 65 \times 7 = 65 \times 7 + (65 \times 4) \times 10$Последнее равенство и является алгоритмом умножения столбиком. Первый сомножитель нужно умножить на последнюю цифру второго сомножителя. Далее первый сомножитель нужно умножить на следующую цифру второго сомножителя - из более старшего разряда. Получившиеся два числа нужно сложить столбиком, предварительно сдвинув второе из них на один разряд вправо. Этот сдвиг в десятичной системе счисления (как и в двоичной, троичной и т.д.) соответствует умножению на $10$: мы не ставим появившийся в конце ноль, поскольку он не повлияет на сумму, а грязи в тетради и на доске будет меньше.
Все школьники рады такому свойству умножения на десять в десятичной системе счисления. Используя это свойство, они заучивают таблицу умножения десятичных цифр, а не чисел. Цифр всего десять, а чисел бесконечно много!
В системе счисления Фибоначчи умножение числа на $10_{f}, 100_{f}, 1000_{f}, \ldots$ является сложной операцией. Поэтому при сложении столбиком записывают все цифры слагаемых, ничего не оставляя в уме.
Пример:
Мы хотим вычислить произведение
${100101}_{f}$ $\times$ $\,{10100}_f$ Попробуем снова разбить второй сомножитель:
$100101_{f} \times 10100_{f} = 100101_{f} \times (F_6 + F_4) =$
$= 100101_{f} \times F_6 + 100101_{f} \times F_4$Полученную сумму складываем столбиком. Значения слагаемых находим выше - в таблице умножения.
${100101}_{f}$ $\times$ $\,{10100}_f$ $\overline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }$ $1010100000_{f}$ $+$ $\,10100101_{f}$ $\overline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }$ ${10010010001}_f$ Деление.
Если умножение есть многократное прибавление одного слагаемого к другому, то деление есть многократное вычитание делителя из делимого. Можно попытаться уменьшить число этих сложений и вычитаний.
В десятичной системе счисления при умножении мы сокращаем число сложений, используя тот факт, что умножать число на цифру можно частично в уме, - используя заклинание «на ум пошло». Этот же приём используется и для сокращения числа вычитаний при делении столбиком. Мы угадываем старшую цифру частного, умножаем ее на делитель и полученное произведение вычитаем из старших разрядов делимого. Здесь мы снова делаем сдвиг влево вычитаемого произведения, позволяя себе не дописывать необходимое число нулей справа, так как они не влияют на результат разности!
Например,
$1221 : 3 = (1221 - (3 \times 400) + (3 \times 400)) : 3 =$
$= (3 \times 400) : 3 + (1221 - (3 \times 400)) : 3$Здесь в первом слагаемом накапливаем частное, а второе продолжаем делить - оно меньше начального делимого. При делении столбиком неполное частное также записывается без правых нулей, чтобы не стирать их при приписывании к нему последующих цифр. В нашем примере записываем не $400$, а $4$.
Продолжаем деление:
$(3 \times 400) : 3 + (1221 - (3 \times 400)) : 3 =$
$= 400 + (1221 - 1200) : 3 = 400 + 21 : 3 =$
$= 400 + 7 = 407$
Здесь один из нулей приходится вспомнить, так как $2 < 3$.В системе счисления Фибоначчи мы не можем так просто жонглировать нулями! Приходится на каждом шаге деления выписывать все цифры вычитаемого числа. В этой системе всего две цифры, но это не упрощает задачу угадывания на каждом шаге деления нужного нам вычитаемого, так как очередная $1$-ца в неполном частном может соответствовать разным числам Фибоначчи.
Пример:
Мы хотим вычислить частное и остаток от деления
$300 = {100100010101}_{f}$ на ${100101}_{f} = 17$.${100100010101}_{f}$ $\underline{| \ {100101}_{f}}$ $|$ В старшем разряде частного должна быть $1$-ца. Какому разряду (числу Фибоначчи) она соответствует? Посмотрим в выше написанную таблицу умножения и найдем в ней наибольшее число Фибоначчи $F_i$ такое, что $M \times F_i = {100101}_{f} \times F_i \le {100100010101}_{f}$. Искомое число Фибоначчи есть $F_7$, значит в частном будет шесть цифр. (Почему?)
Из этой же таблицы находим первое вычитаемое:
${100100010101}_{f}$ $\underline{| \ {100101}_{f}}$ $-$ ${10101000001}_{f}$ $| \ {1}_{f}$ После вычитания получаем: (проверьте!)
${1001000100}_{f}$ $\underline{| \ {100101}_{f}}$ $\; | \ {1 \ldots}_{f} $ Здесь ${1001000100}_{f} = 79$. Продолжаем деление. Ищем в таблице наибольшее число $F_i$ такое, что $M \times F_i \le {1001000100}_{f}$. Это число равно $F_4$. Выше мы выяснили, что искомое частное содержит $6$ цифр, значит перед цифрой $1$, соответствующей числу $F_4$, стоят два ноля. (Почему?)
Из таблицы находим вычитаемое:
${1001000100}_{f}$ $\underline{| \ {100101}_{f}}$ $-$ ${10100101}_{f}$ $| \ {1001}_{f} $ После вычитания получаем: (проверьте!)
${1001010}_{f}$ $\underline{| \ {100101}_{f}}$ $\ \, | \ {1001\ldots}_{f} $ Здесь ${1001010}_{f} = 28$. Продолжаем деление. Ищем в таблице наибольшее число $F_i$ такое, что $M \times F_i \le {1001010}_{f}$. Это число равно $F_2 = 1$. Значит перед цифрой $1$, соответствующей числу $F_2$, стоит один ноль. (Почему?)
Чтобы получить остаток от искомого деления нужно вычесть: (проверьте!)
${1001010}_{f}$ $\underline{| \ {100101}_{f}}$ $-$ $\,{100101}_{f}$ $| \ {100101}_{f} $ $\overline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ }$ $\,{10100}_{f}$
Остаток равен $11 = {10100}_{f}$Ответ:
${100100010101}_{f}$ $\underline{| \ {100101}_{f}}$ $-$ $\underline{{10101000001}_{f}}$ $| \ {100101}_{f}$ ${1001000100}_{f}$ $- \ \ \underline{{10100101}_{f}}$ ${1001010}_{f}$ $- \ \ \,{100101}_{f}$ $\overline{\ \ \ \ \ \ \ \ \ \ \ \ \ \ }$ $\,{10100}_{f}$
То есть частное есть ${100101}_{f}$, а остаток есть $\,{10100}_{f}$. $\Box$ (Сделайте проверку!)Подведем итоги. Показанные алгоритмы умножения и деления в системе Фибоначчи плохие. Причина этого состоит в том, что идеи этих алгоритмов взяты из десятичной системы счисления. Но свойства десятичной системы и системы счисления Фибоначчи существенно отличаются друг от друга.
Исследовательская задача.
Попробуйте придумать хорошие алгоритмы умножения и деления в системе Фибоначчи. - Как поделить торт, не завидуя друг другу? 4 декабря, 2016 г.
Приближаются январские каникулы. Саша уже давно отсчитывает недели и дни до этих новогодних каникул.
Зная о предстоящих подарках, Саша задумался о том, как бы их поделить, чтобы не завидно было. Он решил сосредоточить все внимание на новогоднем торте, поскольку елку ломать на несколько частей - все равно что праздник под корень подрубить.
Поставленная Сашей задача является сложной задачей. Попробуем ему помочь решить ее, хотя бы в упрощенной постановке условия.
Уточнение постановки задачи.
(1) Пусть торт делят два школьника.
(2) Торт неоднороден. Повар намешал в него и малинового варенья, и меда, и заморского инжира, и переславской черники, и еще всякой вкусной всячины. Перемешал он всю эту снедь старательно - и вверх и вниз, и вправо и влево, и из одного угла к другому и т.д.
(3) Торт разрешаем резать как угодно, кромсая его на куски и вырезая затейливые узоры и вбок и поперек, и вверх и вниз. Эти-то куски и будут забирать себе наши школьники.
(4) У каждого школьника свой вкус. Для разных школьников эти вкусы могут совпадать, могут не совпадать, могут вообще не пересекаться - как угодно. Например, один из них любит малиновое варенье с ягодами черники, а второй предпочитает инжир, обмазанный малиновым вареньем. Важно то, что свои вкусы - предпочтения школьники должны хранить втайне друг от друга. В этом случае поводов завидовать друг другу у них будет меньше!
(5) Чтобы школьники не поссорились, деля этот торт, судьей назначим Деда Мороза. Все требования Деда Мороза должны выполняться беспрекословно. Он, в свою очередь, должен судить честно - не подсуживая. Вкусы школьников Дед Мороз не знает. Дед Мороз объявляет, кто из школьников разрезает куски торта первым, вторым и т.д. Школьник может забрать какие-то отрезанные куски, тоже только если Дед Мороз разрешил ему это сделать. Дед Мороз может потребовать выбирать куски не из всех кусков торта, уже отрезанных и не поделенных, а только из некоторых из них. Способ разрезания каких-то кусков тоже может зависеть от указаний Деда Мороза.
После сделанных выше уточнений, постановка задачи становится нижеследующей.
Постановка задачи для двух школьников.
Дан неоднородный торт. Требуется придумать конечную последовательность указаний Деда Мороза, не нарушающих вышеописанные правила, таких, чтобы весь торт был поделен между школьниками и школьники не завидовали бы друг другу. То есть каждый из них, получив свою долю, был бы уверен в том, что сумма доставшихся ему кусков торта содержит не меньше предпочитаемых им вкусностей, чем сумма кусков, которые забрал другой школьник.Решение задачи для двух школьников.
Первого школьника обозначим $p_1$, второго - $p_2$.
(1) Дед Мороз отдает право первого разрезания торта школьнику $p_1$ и говорит ему, что торт нужно разрезать на две части так, чтобы каждая из этих частей, с точки зрения предпочтения разрезающего школьника, была не хуже другой части торта.
(2) Второй ход делает $p_2$. Он должен выбрать себе лучший (точнее, не худший) кусок торта из двух имеющихся.
(3) Третьим ходом школьник $p_1$ забирает оставшийся кусок. Торт полностью поделен.
Почему никто никому не завидует?
$p_2$ сам выбирает из двух кусков лучший кусок. Так что же ему завидовать? С другой стороны, $p_1$ знает что оба куска равнозначны с точки зрения его предпочтений, так что, какой бы кусок ему ни достался, он не в обиде!
Задача решена. $\Box$Теперь рассмотрим аналогичную задачу для трех школьников.
Постановка задачи для трех школьников.
Даны неоднородный торт и три школьника $p_1, p_2, p_3$. Требуется придумать конечную последовательность указаний Деда Мороза, не нарушающих вышеописанные правила, таких, чтобы весь торт был поделен между $p_1, p_2, p_3$ и школьники не завидовали бы друг другу. То есть каждый из них, получив свою долю, был бы уверен в том, что сумма доставшихся ему кусков торта содержит не меньше предпочитаемых им вкусностей, чем каждая из сумм кусков, которые достались двум другим школьникам.Эта задача сложнее, чем решенная выше. Для того чтобы удобней было понимать Деда Мороза, отрезанным кускам торта будем давать названия. По той же причине торт будем считать прямоугольником, тогда мы сможем нарисовать его.
(1) Первый ход аналогичен ходу в решении задачи для двух школьников. Дед Мороз отдает право первого разрезания торта школьнику $p_1$ и говорит ему, что торт нужно разрезать на три части так, чтобы каждая из этих частей, с точки зрения предпочтения разрезающего школьника, была не хуже каждой из оставшихся частей торта.
Обозначим эти части $S_1, S_2, S_3$ и написанное в предыдущем предложении длинное утверждение о свойствах кусков обозначим кратко: ${\it v_1}(S_1) = {\it v_1}(S_2) = {\it v_1}(S_3)$. Здесь ${\it v_1}(S_2)$ есть оценка качества куска куска $S_2$ с точки зрения игрока $p_1$. Аналогичные обозначения будут также использоваться ниже.(2) Второй ход отдается игроку $p_2$. Дед Мороз сообщает ему в записке, что он должен расположить уже имеющиеся куски торта в порядке своего предпочтения, переименовать их согласно этому порядку, но никому не сообщать причины переименования. То есть ${\it v_1}(S_1) \ge {\it v_1}(S_2) \ge {\it v_1}(S_3)$. Где данные на первом шаге имена присвоены уже (возможно) другим кускам торта. Ниже используется эта переименовка.

(3) Третьим ходом школьник $p_2$ продолжает свою игру. Он должен от лучшей части $S_1$ отрезать кусок $S_1'$, равный по значимости куску $S_2$. Остаток обозначим $R$ - он может оказаться пустым. О свойстве ${\it v_2}(S_1') = {\it v_2}(S_2)$ знают только Дед Мороз и игрок $p_2$.
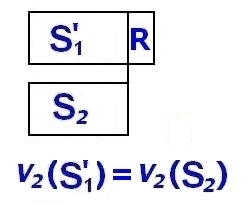
(4) Далее Дед Мороз предоставляет право выбора больших кусков $S_1', S_2, S_3$ в следующем порядке $p_3, p_2, p_1$ (т.е. в обратном порядке). Каждый игрок должен забрать один из кусков, согласно своему вкусу, с одним дополнительным условием. Штрихованный кусок $S_1'$ не должен достаться первому игроку, то есть его должен забрать кто-то из игроков $p_2, p_3$. Но это не обременительно для $p_3$, поскольку он выбирает первым.
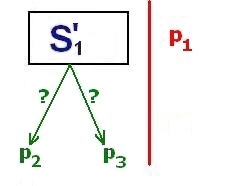
Обозначим $p_A \in \{ p_2, p_3 \}$ того из игроков, кто забрал кусок $S_1'$, и $p_B \in \{ p_2, p_3 \}$ того из игроков, кто не забрал кусок $S_1'$.
(5) Игрок $p_B$ разрезает оставшийся кусок $R$ на три части так, что верны равенства: ${\it v_B}(R_1) = {\it v_B}(R_2) = {\it v_B}(R_3)$. Об этом свойстве знают только Дед Мороз и игрок $p_B$.
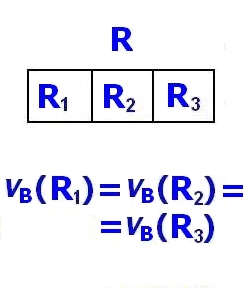
(6) Далее порядок выбора кусков $R_i$ такой: $p_A, p_1, p_B$. Каждый игрок должен забрать один из кусков.
Весь торт поделили!
Утверждение: Никто никому не завидует.
Доказательство.
$p_A$) Рассмотрим игрока $p_A \in \{ p_2, p_3 \}$. Какой бы кусок $R_j$ из маленьких частей он не выбрал, он себя не обидит, поскольку он выбирает первым: ${\it v_A}(R_j) \ge {\it v_A}(R_i)$, где $i \neq j$.
Если $p_A = p_2$, тогда $p_2$ забрал кусок $S_1'$, но ${\it v_2}(S_1') = {\it v_2}(S_2) \ge {\it v_2}(S_3)$ (см. шаги 2 и 3). Значит $p_2$ выбрал лучший из больших кусков и лучший из маленьких. Он более чем доволен.
Если $p_A = p_3$, тогда $p_A$ первым выбирал из больших кусков (см. шаг 4) и первым выбирал из маленьких кусков (см. шаг 6). Он, конечно, себя не обидел.$p_1$) Рассмотрим игрока $p_1$. При выборе больших кусков он возьмет либо $S_2$, либо $S_3$. Но ${\it v_1}(S_2) = {\it v_1}(S_3) \ge {\it v_1}(S_1')$ (см. шаги 1 и 3). И выбором большого куска он не обижен. Более того,
${\it v_1}(S_2) = {\it v_1}(S_3) = {\it v_1}(S_1') + {\it v_1}(R_1) + {\it v_1}(R_2) + {\it v_1}(R_3)$ (см. шаг 3). На игрока $p_A$ игрок $p_1$ не обидится, даже если не возьмет ни одного из маленьких кусков, поскольку ${\it v_1}(S_2) = {\it v_1}(S_3) \ge {\it v_1}(S_1') + {\it v_1}(R_j)$ для любого $j$. На игрока $p_B$ он не в обиде, так как из кусков $R_i$ он выбирает раньше чем $p_B$, поэтому и маленький кусок (как и большой кусок) $p_1$ возьмет не хуже того из $R_i$, который достанется игроку $p_B$.$p_B$) Осталось разобраться с игроком $p_B \in \{ p_2, p_3 \}$. Он сам разрезал кусок $R$ (см. шаг 5), так что имеем: ${\it v_B}(R_1) = {\it v_B}(R_2) = {\it v_B}(R_3)$.
Если $p_B = p_2$, тогда $p_2$ выбрал $S_2$, и он (см. шаги 2 и 3) не завидует тому, что игрок $p_1$ забрал кусок $S_3$; как и тому, что игрок $p_3$ забрал кусок $S_1'$. Так как ${\it v_2}(S_2) \ge {\it v_2}(S_3)$ и $ {\it v_2}(S_2) \ge {\it v_2}(S_1')$. Следовательно, если игрок $p_2$ забрал $j$-ый кусок $R_j$, тогда $({\it v_2}(S_2) + {\it v_2}(R_j)) \ge ({\it v_2}(S_3) + {\it v_2}(R_i))$ и $ ({\it v_2}(S_2) + {\it v_2}(R_j)) \ge ({\it v_2}(S_1') + {\it v_2}(R_i))$, где $i \neq j$.
Если $p_B = p_3$, тогда он первым выбирал из больших кусков и его устраивает любой из кусков $R_i$. Так что он себя не обидел!Утверждение доказано. $\Box$
Аналогичная задача для четырех игроков решена только в сентябре 2016 года, и предложенное решение состоит из примерно двухсот шагов. Доказано, что для любого $n > 4$ решение задачи для $n$ игроков существует, но никто не знает явного описания этих решений.
Домашняя исследовательская задача.
Даны неоднородный торт и пять школьников. Требуется придумать конечную последовательность указаний Деда Мороза, не нарушающих вышеописанные правила, таких, чтобы весь торт был поделен между этими школьниками и они не завидовали бы друг другу. - Дуэль! 15 января, 2017 г.
Боцман, помощник корабельного комиссара (далее для краткости - Завхоз) и мичман Изи решили провести «тройственную дуэль» каждый против всех.
Порядок дуэли следующий. Дуэль проходит по раундам до полной победы одного из участников - как у гладиаторов в древнем Риме. Жребий определяет, кто стреляет первым, кто вторым и кто третьим в первом раунде. Тот, в кого попали, из дуэли выбывает, а остальные продолжают стрелять по очереди. Определенная жребием очередность стрельбы сохраняется, пока из дуэли не выбывают все участники, кроме одного. Лучше всех из участников поединка стреляет боцман - он никогда не промахивается. Завхоз попадает в цель в $8$ из $10$ случаев, а мичман Изи - лишь в половине. Каждый из них знает, как стреляют остальные, и старается действовать так, чтобы увеличить свои шансы на победу.
Как будет проходить дуэль и кто, скорее всего, в ней победит?
Будем представлять историю дуэли в виде дерева: в его вершинах запишем действие участника, которому пришла очередь стрелять, а ребра, соответствующие удачному и неудачному исходам выстрела, пометим шансами, соответствующими этим исходам. Шанс на то, что развитие дуэли достигнет некоторой вершины в дереве, есть произведение чисел, стоящих на ребрах пути, ведущих из корня дерева к этой вершине.
(1) Пусть жеребьевка определила, что первым будет стрелять боцман (Б). Поскольку Боцман никогда не промахивается, а значит, после своего выстрела он оказывается один на один с оставшимся соперником, ему выгодно устранить более сильного - завхоза (З). После чего, если мичман Изи (МИ) не пристрелит боцмана в свою очередь (а она наступит сразу же после выстрела боцмана), боцман с гарантией пристрелит мичмана Изи. Дерево исходов дуэли (рисунок 1) для стреляющего первым боцмана выглядит следующим образом (в квадратах - имена победителей дуэли).
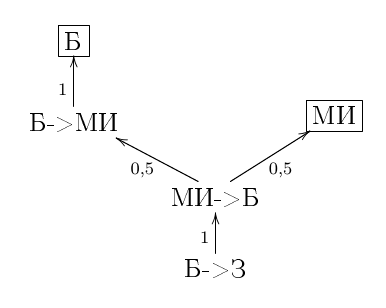
Рисунок 1При этом в $50\%$ случаев (если мичман Изи промахнулся) в дуэли выигрывает Боцман, а в $50\%$ - мичман Изи.
(2) Пусть первым стреляет завхоз. Если он выстрелит в мичмана Изи и попадет в него, то будет заведомо пристрелен боцманом. В этом случае шансов на победу у завхоза не будет. Если он выстрелит в боцмана и попадет в него, то следующим будет стрелять мичман Изи. С шансом $50\%$ он попадет в завхоза и выиграет дуэль. Однако остается еще шанс $50\%$, что мичман Изи промахнется, и тогда следующим выстрелом завхоз пристрелит его с шансом 80%. Таким образом, в этом случае шанс на победу завхоза есть как минимум $0,5 \times 80\%=40\%$. Теперь посмотрим, что случится, если завхоз промахнётся (неважно, в кого). Если по жеребьевке следующим стреляет боцман, он сразу же пристрелит завхоза (см. пункт 1). Если стреляет мичман Изи и промахивается, происходит то же самое. Самая лучшая возможность для завхоза в случае его промаха - если после него наступит очередь мичмана Изи, тот решит стрелять в боцмана и попадёт. Однако такое поведение невыгодно для мичмана Изи (см. пункт 3). Поэтому завхозу выгоднее стрелять в боцмана, чем в мичмана Изи, и выгоднее попасть, чем промахнуться.
(3) Пусть настала очередь мичмана Изи стрелять, и оба его соперника живы. Если он решит стрелять в завхоза и попадёт в него, то будет немедленно пристрелен боцманом. Если промахнётся - действия пойдут по сценариям, описанным в пунктах 1 или 2. Если мичман Изи успешно выстрелит в боцмана, то с вероятностью $80\%$ будет пристрелен завхозом. Если же промахнётся - действия опять пойдут по сценариям, описанным в пунктах 1 или 2. Значит, мичману Изи в любом случае выгоднее промахнуться, чем попасть в соперника, и наилучшей стратегией для него будет стрелять в воздух до тех пор, пока кто-нибудь из боцмана или завхоза не будет пристрелен другим.
В половине случаев (если жеребьевка определила боцману стрелять раньше завхоза) при таком поведении мичмана Изи сценарий будет развиваться, как описано в пункте 1, в половине - как описано в пункте 2. Фрагмент истории возможных исходов дуэли будет выглядеть следующим образом (рисунок 2).
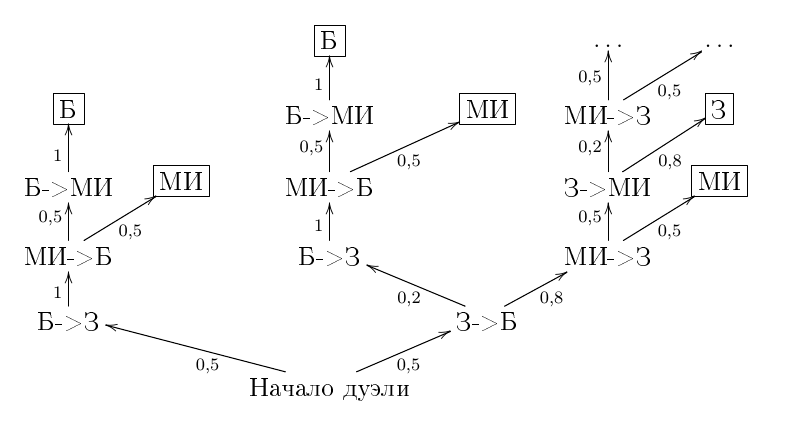
Рисунок 2Посчитаем теперь шансы каждого участника дуэли на победу. Легче всего это сделать для боцмана. Два пути в дереве истории дуэлей ведут к его победе. Шансы этих побед равны $0,5 \times 0,5 = \frac{1}{4}$ и $0,5 \times 0,2 \times 0,5 = \frac{1}{20}$. Общий шанс победить равен сумме шансов этих двух возможностей - а именно $\frac{3}{10}$.
Листьев дерева, соответствующих победам завхоза, будет бесконечно много (они с мичманом Изи могут промахиваться друг в друга сколько угодно раз). Тем не менее, можно заметить, что каждый парный промах происходит с шансом $0,2 \times 0,5 = 0,1$ (завхоз промахивается в $20\%$ случаев, а мичман Изи промахивается в половине случаев), поэтому сумма всех шансов на победу завхоза есть $0,5 \times 0,8 \times 0,5 \times 0,8 \times (1+0,1+0,001+\ldots)$, или, если записать результат в виде периодической дроби, $0,4 \times 0,(4)$. Последняя есть $0,(1) \times 4$, а $0,(1)$ - десятичное представление дроби $\frac{1}{9}$. Поэтому общие шансы на победу завхоза равны $\frac{2}{5} \times \frac{4}{9}=\frac{8}{45}$.
Шансы на победу мичмана Изи теперь вычислим, вычтя из $1$ шансы на победу двух других участников дуэли. Получаем $1-\frac{3}{10}-\frac{8}{45}=\frac{47}{90}$. Самый плохой стрелок имеет в тройственной дуэли шанс победить, не только больший, чем у других, но и несколько больший половины!
Положение самого слабого, защищающее мичмана Изи в самом начале дуэли (и дающее возможность выстрелить первым при переходе к дуэли один на один), дает ему весомые преимущества против более сильных. Чем лучше стреляет мичман Изи, оставаясь при этом самым плохим стрелком из трёх, тем вернее ему достанется победа.
|
Андрей Немытых, nemytykh@math.botik.ru |
Институт программных систем РАН,
г. Переславль-Залесский
http://www.botik.ru/pub/local/scp/refal5/
