Материалы занятий
- 20 сентября, 2015 г.
Знакомство со школьниками и их родителями.
Теорема Пифагора: в любом прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Доказательство теоремы Пифагора методом разрезаний двух квадратов со сторонами, равными гипотенузе прямоугольного треугольника. - 27 сентября, 2015 г.
Рассмотрим на клетчатой бумаге квадрат размером 8х8 клеток и прямоугольник размером 13x5 клеток. Оказывается, что из кусков указанного выше квадрата «можно сложить» указанный выше прямоугольник, хотя этот прямоугольник состоит из 65 клеток, а квадрат из 64 клеток. Мы попытаемся понять это противоречивое построение, т.е. найти в нем ошибку.
Двоичиным деревом называется дерево, у которого из каждой точки ветвления выходит ровно две ветви. Корень дерева также является точкой ветвления. Высотой дерева назовем количество шагов, опирающихся на ветвления, которые нужно сделать, чтобы добраться до самого дальнего листа в этом дереве. Какое максимальное количество листов может висеть на дереве высоты 4?Видео-запись занятия кружка / 27 сентября 2015 г. - Системы счисления. 4 октября, 2015 г.
В хозяйстве тети Тани из села Веськово один петух контролирует 25 куриц. Тетя Таня уверена, что петух не ошибется в подсчете своих куриц, несмотря на то что у петуха по четыре пальца на каждой ноге, и отстоит их от посягательства соседского петуха. Тетю Таню, однако, поразили записи на песке, привезенном с берега озера Плещеево. Она смогла их переписать, хотя и были они написаны лапой курицы. Тетя Таня уверена, что обнаруженная запись обозначает, сколько в ее хозяйстве куриц, но эта запись на песке никак не напоминала число 25. Помогите тете Тане избавиться от бессонницы, которая у нее возникла от обдумывания этого парадокса.
Космонавты российской космической экспедиции на Марсе сообщили на Землю, что марсиане оказались шестипалыми. Они обнаружили на Марсе явные следы древнего человека: на ценниках в марсианских магазинах использовались все арабские цифры, без которых и на Земле не обходятся. Но не трудно было понять, что земные предки марсиан примарсились на коврах-космолетах несколько сот миллионов лет назад. Непривычные физические условия жизни повлияли на генетический код, образовав шестипалую цивилизацию. Яблони, занесенные землянами, прижились на Марсе и давали превосходный урожай. Кроме арабских цифр, ценники на марсианские яблоки содержали два неизвестных для космонавтов магических знака. Космонавты решили, что марсианская математическая школа давно обогнала математическую школу землян и использует эти два магических знака для выражения законов математики, которые пока еще не открыты на Земле. Магические знаки были сфотографированы и переданы на механико-математический факультет Московского государственного университета для тщательного изучения. Нашим кружковцам требуется помочь мех-мату МГУ разработать новую математическую теорию и понять, где яблоки продаются дешевле, - в Переславле или на Марсе.

Итоги конкурса «Начертание марсианских цифр». Ищем автора названия марсианской валюты! Видео-запись занятия кружка / 4 октября 2015 г. - Системы счисления (продолжение). 11 октября, 2015 г.
Можно рассматривать системы счисления с разными основаниями. На предыдущем занятии мы изучали системы счисления с основанием 8 и 12. В информатике используются, например, двоичная система счисления, шестнадцатеричная система система счисления и даже система счисления с основанием $2^{32}$, в которой $2^{32}$ цифр. Были экспериментальные попытки создать вычислительную машину, работающую в системе счисления по основанию 3. Системы счисления, аналогичные десятичной, называются позиционными, т.к. смысл цифр в записи числа зависит от позиции этих цифр. Например, в записи числа 121 первая цифра 1 означает количество сотен в числе, а последняя цифра 1 - количество единиц в этом числе.
Самая простая система счисления - единичная. Её изучают в детском саду, когда проходят основы счета, с использованием палочек. Эта система не является позиционной. Римская система счисления тоже не является позиционной.
Правила арифметики в позиционных системах счисления не зависят от основания системы счисления. Например, вы можете складывать столбиком числа, записанные в восьмеричной системе. Однако нужно помнить, что в этой системе счисления нет цифр 8 и 9. От этого зависит то, что «на ум пойдёт».
Цифры десятичной системы счисления были изобретены арабской цивилизацией. Две цифры марсианской системы счисления изобретены нашими кружковцами. В данное время землянами в основном используются арабские цифры.
Здесь можно посмотреть китайские цифры, а здесь - славянские цифры. И те, и другие ещё иногда используются. Славянские цифры и числа можно увидеть на циферблате башенных часов в Суздале. Если наши кружковцы посетят рынок в городе Ухань (центр китайской провинции Хубей), то обнаружат, что они не понимают цен даже тогда, когда продавцы, опознав в них чужестранцев, начнут показывать цены на пальцах.
Видео-запись занятия кружка / 11 октября 2015 г. - Длина записи числа. 18 октября, 2015 г.
Рассмотрим два произвольных целых положительных числа A и B, их сумму A+B и произведение A×B. Длина записей этих чисел зависит от основания позиционной системы счисления, в которой они записаны. Например, длина записи четвёрки в десятичной системе счисления равна 1, а в двоичной системе счисления равна 3 (здесь обе длины записаны в десятичной системе счисления).
Оказывается, какую бы позиционную систему счисления мы ни использовали, длина суммы A+B, с точностью до единицы, равна длине большего числа из A и B. А длина произведения A×B, с точностью до единицы, равна сумме длин сомножителей.
Пусть дл(N) обозначает длину записи целого положительного числа N в некоторой позиционной системе счисления. Утверждение о длинах записей чисел можно уточнить.
Утверждение 1. В любой позиционной системе счисления max(дл(A), дл(B)) ≤ дл(A+B) ≤ max(дл(A), дл(B)) + 1, где max(дл(A), дл(B)) обозначает наибольшую из двух длин дл(A), дл(B).
Утверждение 2. В любой позиционной системе счисления дл(A) + дл(B) - 1 ≤ дл(A×B) ≤ дл(A) + дл(B).
Т.е. длина суммы двух целых положительных чисел может быть больше длины каждого из слагаемых только на единицу, а длина произведения двух целых положительных чисел примерно равна сумме длин сомножителей.
Таким образом, длина суммы двух целых положительных чисел почти не отличается от длины наибольшего из слагаемых, а чтобы примерно вычислить длину произведения двух целых положительных чисел, нужно просто сложить длины сомножителей. И эти утверждения не зависят от основания позиционной системы счисления!
А как изменяются длины чисел при сложении и умножении в единичной системе счисления?
Видео-запись занятия кружка / 18 октября 2015 г. - Взвешивания на весах с двумя чашками. 25 октября, 2015 г.
Султан объявил конкурс на самый лучший разновес для взвешивания пряностей от 1 до 100 граммов. Этот разновес он собирался покрыть золотом и установить у себя во дворце в качестве эталона. К султану пришёл народный умелец и предложил набор из десяти гирь для разновеса. Удастся ли кружковцам предложить султану разновес лучше, чем у народного умельца?
В 1797 году в Российской Империи был выпущен указ, устанавливающий разновес из гирь в золотниках, фунтах и пудах. Это единственный разновес в истории, включавший в себя наименьший возможный набор гирь для взвешивания на весах с двумя чашками. Кружковцы попробуют себя в роли купца 1800 года, потерявшего таблицу для взвешивания, и познакомятся с троичной симметричной системой счисления, использовавшейся в советской вычислительной машине «Сетунь».
Справка: Сетунь - река и вычислительная машина.
Видео-запись занятия кружка / 25 октября 2015 г. - Сравнение длин записей числа в разных системах счисления.
1 ноября, 2015 г.Современные вычислительные машины используют двоичную систему счисления. В память этой машины, реализованной в виде набора микро-схем, можно поместить определенное количество цифр (в данном случае - двоичных). А значит, еще меньше чисел, составленных из этих цифр.
Мы рассмотрим следующий вопрос: во сколько раз больше цифр можно поместить в тот же физический объём микро-схемы, если использовать троичную или другие системы счисления? Например, системы счисления по основаниям: 10, 100, 1000, 4, 8, 16, 9, 27.
Оказывается, есть очень простой способ преобразования записи числа в системе счисления по основанию β в систему счисления по основанию β$^n$.
Видео-запись занятия кружка / 1 ноября 2015 г. - Сравнение длин записей числа в разных системах счисления
(продолжение). 8 ноября, 2015 г.Пусть положительное натуральное число $N$ записано в системе счисления по основанию $\beta > 1$. Пусть $дл(N_{(\beta)})$ означает длину числа $N$ в системе счисления по основанию $\beta$. Пусть $k > 1$ - некоторое натуральное число, тогда $дл(N_{(\beta^k)})$ - длина числа $N$ в системе счисления по основанию $\beta^k$ удовлетворяет неравенствам:
$дл(N_{(\beta)})/k \le дл(N_{(\beta^k)}) \le [дл(N_{(\beta)})/k] + 1$
Здесь посредством $[N/k]$ обозначена целая часть частного от деления $N$ на $k$. Например, $[5/2] = 2$ (так как при делении $5$ на $2$ получаем $2$ и в остатке $1$). Другие примеры: $[4/2] = 2$ , $[10/3] = 3$ , $[4/5] = 0$.
В двоичной системе счисления $дл(2^{2015}_{(2)}) = 2016$ , длина этого числа в системе счисления по основанию $2^{2015}$ равна $дл(2^{2015}_{(2^{2015})}) = 2$. Мы увеличили основание системы счисления в $2^{2014}$ раз, а длина уменьшилась в $2016/2 = 1008$ раз.
Откуда получаем:
$2^{2014} = 2^{2010 + 4} = 2^{10 \times 210 + 4} = (2^{10})^{210} \times 2^4 =$
$= 1024^{210} \times 16 > 1000^{210} \times 16$.
Следовательно, основание системы мы увеличили больше чем в $16000...0$ раз (здесь после числа $16$ стоят $630$ нулей), а длина числа уменьшилась всего лишь в $1008$ раз.
Видео-запись занятия кружка / 8 ноября 2015 г. - Зеркальные отражения. 15 ноября, 2015 г.
Всем известно, что кратчайший путь между двумя точками $A$ и $B$ на плоскости проходит по прямой, соединяющей эти две точки.
Рассмотрим прямую дорогу между $A$ и $B$. Если перегородить эту дорогу зеркалом, то мы увидим, что дорога изломается. На ней появится крутой поворот в виде угла, величина которого зависит от угла между плоскостью зеркала и дорогой. При этом длина изломанной дороги останется равной длине прямой дороги.
Таким же способом можно выпрямить дорогу, состоящую из двух прямых отрезков, расположенных под углом к друг другу.
Действительно, в точке поворота этой дороги поставим зеркало, и будем его поворачивать, пока не увидим, что путь до зеркала и отражение в зеркале той части пути, которая идет за поворотом, не оказались на одной прямой линии. Длина всего пути опять не изменилась.
Видео-запись занятия кружка / 15 ноября 2015 г. - Зеркальные отражения (продолжение). 22 ноября, 2015 г.
С помощью зеркальных отражений некоторых фигур можно замостить площадь (или застелить пол паркетом).
Оказывается, что изучение паркета из одинаковых равносторонних треугольников помогает решить следующую задачу.
Улей огородили забором в виде равностороннего треугольника. Где точно находится улей внутри этого треугольника, неизвестно. Дети пасечника намазали одну из внутренних сторон этого треугольника клубничным вареньем, другую - малиновым, а третью - мёдом.
У пчелы много пчелят. Некоторые из них любят мёд, некоторые - клубничное варенье, а некоторые - малиновое. Пчела, захватив три ведра, вылетает из улья, чтобы принести деткам все три вида сладостей. По какому пути нужно лететь пчеле, чтобы как можно быстрее накормить пчелят?
Видео-запись занятия кружка / 22 ноября 2015 г. - Признаки остатков от деления на целые числа.
29 ноября, 2015 г.Признаки деления целых чисел на данное положительное целое число $k$ просто обобщаются до признаков остатков при делении этих чисел на $k$. В школе рассказывают про признаки деления на $2, 3, 5, 9, 10$. Мы приведем только некоторые из признаков остатков. Про другие читатель легко догадается сам.
Признак остатка при делении на $3$. Остаток от деления целого числа $N$ на $3$ равен остатку от деления суммы цифр числа $N$ на $3$.
Признак остатка при делении на $11$. Остаток при делении целого числа $N$ на $11$ равен остатку при делении знакопеременной суммы цифр числа $N$ на $11$. Т.е. если $N = \overline{a_n a_{n-1}\ldots a_1 a_0}$, тогда остаток при делении $N$ на $11$ равен остатку при делении суммы $a_0 + (-1)^1 \times a_1 + \ldots + (-1)^{n-1} \times a_{n-1} + (-1)^n \times a_n$ на $11$.
Нетрудно также доказать следующий признак остатка при делении произведения двух данных целых чисел на одно и то же положительное целое число $k$.
Утверждение 1. Пусть даны три целых положительных числа $N$, $M$ и $k$. Обозначим остаток от деления $N$ на $k$ через $r_1$, а остаток от деления $M$ на $k$ через $r_2$. Тогда остаток от деления произведения $N \times M$ на $k$ равен остатку от деления произведения $r_1 \times r_2$ на $k$.
Видео-запись занятия кружка / 29 ноября 2015 г. - Настольные игры с двумя участниками. 6 декабря, 2015 г.
Пусть, как обычно, игроки ходят по очереди - один за другим. Но кто ходит первым? - Этот вопрос школьниками решается посредством жребия, «бросание» которого можно организовать разными способами.
А что произойдет, если кому-то дать право выбора хода? Т.е. один из игроков решает, будет ли первый ход делать он сам или его соперник.
Мы рассмотрим примеры простейших игр, когда такое право выбора обеспечивает победу, если выбравший свой ход игрок не ошибается.
Видео-запись занятия кружка / 6 декабря, 2015 г. - Настольные игры с двумя участниками (продолжение).
13 декабря, 2015 г.Выигрышные стратегии в играх часто описываются в математических терминах. Поэтому свободное владение конкретной стратегией требует от игрока владения элементами математической культуры.
Мы рассмотрим две игры. Выигрышная стратегия в первой игре использует понятие центральной симметрии на плоскости относительно выбранной точки. Чтобы победить во второй игре, нужно свободно владеть понятием остатка при делении одного натурального числа на другое.
Видео-запись занятия кружка / 13 декабря, 2015 г. - Игры на двоичном дереве. 20 декабря, 2015 г.
Можно играть и на двоичном дереве, по очереди передвигая фишку вверх по дереву - из одного ветвления в другое. Цель таких игр может быть разной. Важно, что снова играют по очереди два игрока. Мы снова разрешим одному из них выбирать право очереди первого (или второго) хода. И снова зададимся вопросом: существует ли выигрышная стратегия для этого игрока?
Оказывается, что во всех до сих пор рассмотренных нами играх, есть общая закономерность, которую кружковцы пока не заметили. Мы раскроем ее на первом занятии в следующей четверти.
Видео-запись занятия кружка / 20 декабря, 2015 г. - Угадывание слов и треугольник Паскаля. 17 января, 2016 г.
Рассмотрим игру со следующими правилами. Ведущий задумывает слово заданной длины. Угадывающий последовательно называет слова такой же длины, про которые ведущий обязан сообщить, сколько букв в них совпадает с задуманным словом. Считаются только буквы, стоящие на местах, совпадающих с местами этих же букв в задуманном слове.
Наилучшую стратегию для такой игры со словами в алфавите большого размера не так просто построить. Но если алфавит содержит только две буквы, то оказывается, что при построении такой стратегии для всех слов вплоть до длины $N$ приходится строить треугольник Паскаля высоты $N$. И в этом же треугольнике можно найти подсказки, как загадать самое трудное слово.
- Передача смс-сообщений по межпланетной мобильной связи.
24 января, 2016 г.Межпланетная мобильная связь настолько дорога, что космонавт Александр, собирающийся в полет на Марс, договорился со своим другом Романом, остающимся на Земле, общаться между Марсом и Землей только смс-ками. Оператор межпланетной связи - монополист Speed-line - установил цены на смс-сообщения пропорционально длине этих сообщений.
Сообщения пересылаются только закодированными в виде натуральных чисел в двоичной системе счисления. Плата берется за пересылку каждой двоичной цифры.
Александр и Роман - заядлые филателисты. Перед полетом Александра они зашли в московский магазин и купили два одинаковых пустых альбома для марок. Один альбом - для Романа, и другой - для Александра. Александр надеется, что в киосках Марс-печать продаются интересные марки.
Друзья хотели бы обмениваться некоторой информацией, зависящей от числа марок в обоих альбомах. Мы будем обсуждать задачи, решение которых позволило бы друзьям экономить деньги при обмене смс-сообщениями, используя услуги оператора Speed-line.
Видео-запись занятия кружка / 24 января, 2016 г. - Двоичные деревья и межпланетная связь. 31 января, 2016 г.
Оказывается, что двоичные деревья иногда могут помочь сэкономить деньги при межпланетных переговорах посредством смс-ок, если вы заранее знаете, какую информацию о марках из двух альбомов - марсианского и земного - вы хотели бы иногда получать от вашего марсианского друга и пересылать ему на Марс.
Видео-запись занятия кружка / 31 января, 2016 г. - Двоичные деревья и межпланетная связь (продолжение).
7 февраля, 2016 г.Для каждой конкретной задачи, которую Александр и Роман хотят решать, прибегая к услугам оператора межпланетной связи Speed-line, они еще до отлета Александра на Марс тщательно обдумывают правила будущих переговоров. Чтобы не запутаться, правила этих переговоров удобно записывать с помощью двоичных деревьев, в которых каждой смс-ке соответствует один шаг от одного ветвления к ближнему вышестоящему ветвлению в дереве.
Выбор конкретной ветви, вдоль которой будет делаться шаг, зависит от того $0$ или $1$ будет пересылаться этим сообщением. В узлах же дерева (точках ветвления) удобно записывать имя того участника переговоров, который будет делать описанный выше шаг по дереву - пересылать конкретную двоичную цифру. Если кто-то добрался до одного из листьев дерева, то следующий ход невозможен (двигаемся только вверх). Следовательно, в этот момент оба наших друга уже должны обладать полным ответом на поставленный ими же вопрос в задаче, которую они решают. Этот ответ мы запишет прямо на соответствующем листе дерева.
На разных листьях могут быть записаны разные ответы, поскольку вдоль путей к этим листьям некоторые сообщения с одного пути не совпадают с сообщениями с другого пути, хотя и написаны на одной и той же высоте от корня дерева. Более того, длина путей от корня к разным листам может быть разной - листья могут находиться на разной высоте.
Видео-запись занятия кружка / 7 февраля, 2016 г. - Понятие наибольшего общего делителя двух целых положительных чисел. 14 февраля, 2016 г.
Пусть даны два произвольных целых положительных числа $a$ и $b$.
Выпишем все делители числа $a$: $1, \ldots,$ ??? $, \ldots, a$. Среди них есть всегда тривиальный делитель $1$, на который делится любое число. Также любое число делится на самого себя. Т.е. тоже является собственным делителем. Если $a \neq 1$, то эти два делителя разные. В общем случае, у числа $a$ могут быть и другие делители, которые мы и обозначили знаками вопроса. Для простых чисел всегда существует ровно два неинтересных делителя, указанных выше.
Множество делителей числа $b$ тоже содержит единицу:
$1, \ldots,$ ??? $, \ldots, b$.
Значит, числа $a$ и $b$ имеют хотя бы один общий делитель. Но может оказаться так, что существуют еще какие-то общие делители чисел $a$ и $b$. Все делители любого числа не больше самого этого числа. Значит, среди общих делителей чисел $a$ и $b$ всегда найдется наибольший общий делитель. Обозначим его НОД$(a, b)$.
Пусть $n$ - какой-то (не обязательно наибольший) общий делитель чисел $a$ и $b$, тогда и число $a - b$ тоже делится на $n$. Если $a > b$, тогда $a - b > 0$ и предыдущее предложение означает, что множество общих делителей чисел $a$ и $b$ совпадает с множеством общих делителей чисел $a$ и $a - b$. Следовательно, наибольший элемент первого из этих множеств совпадает с наибольшим элементом второго из этих множеств:
НОД$(a, b)$ $=$ НОД$(a - b, b)$ Но, поскольку $a - b < a$ , то пара чисел $a - b$, $b$ проще начальной пары $a$, $b$. А значит и НОД$(a - b, b)$ можно вычислить проще! Но, вычислив НОД$(a - b, b)$, мы узнаем и НОД$(a, b)$, так как они совпадают.
Таким образом, если требуется вычислить НОД$(a, b)$, где $a > b$, то мы можем вместо него вычислять НОД$(a - b, b)$. Далее, если $a - b = b$, то НОД$(a - b, b)$ $=$ $b$. Иначе, одно из чисел $a - b$, $b$ больше другого, и мы можем снова упростить задачу, как это уже было сделано выше. Поскольку каждый раз хотя бы оно из двух чисел, рассматриваемой пары, уменьшается и оба числа положительные, то количество шагов упрощения не может быть больше чем $a$ (напомним, что $a > b$).
Почему?
- Алгоритм Евклида. 21 февраля, 2016 г.
Алгоритм вычисления наибольшего общего делителя двух данных положительных целых чисел, который мы разобрали на предыдущем уроке, можно упростить - уменьшить число шагов этого алгоритма.
Действительно, если $a > b > 0$, то НОД$(a,b)$ $=$ НОД$(a - b, b)$. И, пока первое из чисел в паре больше второго, мы можем продолжать это равенство:
НОД$(a, b)$ $=$ НОД$(a - b, b)$ $=$ НОД$(a - b - b, b)$ $=$ НОД$(a - b - b - b, b)$ $=$ $\ldots$ На каком-то шаге первое из очередной пары чисел окажется меньше, чем $b$. Это число равно остатку от деления $a$ на $b$. Почему?
Следовательно, мы сразу можем найти остаток от деления $a$ на $b$. Обозначим его $r$. Этот остаток меньше $b$.
Если $r = 0$, тогда НОД$(a, b)$ $=$ $b$. Так как оказалось, что не только $b$, но и $a$ делится на $b$!
Иначе $0 < r < b$, и мы можем продолжить вычисления уже с парой чисел $b$ и $r$:
НОД$(a, b)$ $=$ НОД$(b, r)$ Этот упрощенный алгоритм вычисления наибольшего общего делителя двух целых положительных чисел называется алгоритмом Евклида (на древнегреческом языке - $E\grave{\upsilon}\kappa\lambda\epsilon\acute{\iota}\delta\eta\varsigma$). Годы жизни Евклида - около 300 года до Рождества Христова.
Видео-запись занятия кружка / 21 февраля, 2016 г. - Признаки делимости, не являющиеся признаками остатков. 28 февраля, 2016 г.
Все, ранее (осенью 2015 года) рассмотренные нами, признаки делимости целых чисел на какое-то конкретное положительное число $k$ являются одновременно и признаками остатков деления этих чисел на число $k$. Например, при делении чисел $123$ и $1+2+3 = 6$ на $9$ получится один и тот же остаток. И, следовательно, он равен $6$.
Мы рассмотрим несколько новых признаков делимости, которые не являются признаками остатков.
Признак делимости на 7: Любое целое число $M > 0$ можно представить в виде следующей суммы $M = 10*a + b$. Число $M$ делится на $7$ тогда и только тогда, когда число $a - 2b$ делится на $7$.
Пример: число $231 = 23*10 + 1$ делится на $7$, так как число $23 - 2 = 21$ делится $7$.
Другой пример: рассмотрим число $125 = 12*10 + 5$. Оно не делится на $7$, так как $12-2*5 = 2$ не делится на $7$. Остаток от деления $125$ на $7$ равен $6$. Остаток от деления $2$ на $7$ равен $2$. То есть эти два остатка не совпадают. Они разные!
Видео-запись занятия кружка / 28 февраля, 2016 г. - Марсианские прямоугольники. 6 марта, 2016 г.
Математическая наука на Марсе продвинулась дальше земной науки.
Земляне по старинке считают прямоугольником только пересечение двух полос, одна из которых параллельна координатной оси $\vec{OX}$, а другая параллельна координатной оси $\vec{OY}$.
Марсиане же уже давно называют прямоугольником объединение попарных пересечений любого числа полос, параллельных оси $\vec{OX}$, с любым числом полос, параллельных оси $\vec{OY}$.

Марсианский математик убедительно просил Сашу хорошо освоить понятие марсианского прямоугольника. Он утверждал, что это поможет Саше и Роману сэкономить деньги на межпланетные смс-пересылки.

Мы попробуем понять, что имел в виду марсианский математик.
Видео-запись занятия кружка / 6 марта, 2016 г. - Закон сохранения энергии. 13 марта, 2016 г.
Получив марсианскую визу, Саша однажды уже побывал на этой далекой от Земли планете. Марс Саше понравился, и он твердо решил сделать свои космические путешествия регулярными. Билет на Марс стоит недешево … Это обстоятельство не дает Саше покоя ни днем, ни ночью.
Он решил изобрести вечный двигатель, который сможет сбить цены на межпланетные перелеты. Вечный двигатель не нуждается не только в дорогих, но и в любых видах топлива.
Все ночи напролет он обдумывает разные варианты конструкций такого двигателя. Рисует эскизы и рвет листы бумаги с неудавшимся решениями поставленной задачи. На уроки приходит с красными глазами и засыпает на парте.
Мы попробует убедить нашего юного космонавта в тщетности его усилий и надеемся таким образом сохранить его здоровье.
Видео-запись занятия кружка / 13 марта, 2016 г. - Теорема об угле, вписанном в окружность. 20 марта, 2016 г.
Мы напомним доказательство школьной теоремы о свойстве угла, вписанного в окружность.
Теорема: угол, вписанный в окружность, равен половине центрального угла, опирающегося на ту же дугу.
На следующем занятии мы будем использовать эту теорему при доказательстве теоремы Коперника.
Видео-запись занятия кружка / 20 марта, 2016 г. - Теорема Коперника. 27 марта, 2016 г.
В утверждение нижеследующей теоремы трудно поверить, пока вы её не доказали.
Теорема Коперника: Пусть по неподвижной окружности, касаясь её изнутри, катится без скольжения окружность вдвое меньшего радиуса. Тогда любая точка $K$, отмеченная мелом на подвижной окружности, движется по диаметру неподвижной окружности.
Другими словами, точка $K$ движется по отрезку прямой линии! И это несмотря на то, что она также одновременно движется по внутренней окружности.
Если изменить соотношение радиусов окружностей, то точка $K$ будет двигаться по сложной кривой.
Видео-запись занятия кружка / 27 марта, 2016 г. - Игры на бесконечной шахматной доске. 10 апреля, 2016 г.
Рассмотрим бесконечную шахматную доску, у которой есть левая и нижняя стороны, но нет ни верхней стороны, ни правой.
На такой доске можно играть в простые игры, подобные двум следующим, выбирая другие шахматные фигуры.
Игра 1. В одной из клеток бесконечной шахматной доски стоит «односторонняя ладья», которая может двигаться влево или вниз. Двое игроков ходят по очереди, сдвигая ладью влево или вниз на любое число клеток (но не менее одной); кто не может сделать ход, проигрывает.
Игра 2. На бесконечной доске стоит «односторонний король», который может сдвигаться на одну клетку влево, вниз или влево-вниз по диагонали. Двое игроков ходят по очереди; кто не может сделать ход (король в левом нижнем углу), проигрывает.
Для этих игр легко найти выигрышные стратегии, если таковые существуют при заданной начальной позиции фигуры.
Вместо плоской шахматной доски можно рассмотреть трёхмерную бесконечную шахматную доску, естественным образом расширив правила, по которым ходят ладьи и короли.
Поиск выигрышных стратегий для аналогичных трёхмерных игр - задача достаточно сложная. Одну из таких игр мы изучим на следующем занятии кружка.
Видео-запись занятия кружка / 10 апреля, 2016 г. - Перекладывание спичек и двоичная система счисления.
17 апреля, 2016 г.Мы продолжаем играть на бесконечных шахматных досках «односторонней ладьёй».
Вместо плоской шахматной доски рассмотрим трёхмерную бесконечную шахматную доску, естественным образом расширив правила, по которым ходит ладья.
Трёхмерная игра. В одной из клеток трёхмерной бесконечной шахматной доски стоит «односторонняя ладья», которая может двигаться влево, вниз или вперёд. Другими словами: в направлении плоскостей стенок трёхмерной доски. Правой и задней стенок у этой шахматной доски нет, как и нет потолка. Двое игроков ходят по очереди, сдвигая ладью влево, вниз или вперёд на любое число клеток (но не менее одной). Кто не может сделать ход, проигрывает.
Найти выигрышную стратегию, если она существует при заданной начальной позиции «односторонней ладьи» сложно. Но понять её легко, если вы выучили двоичную систему счисления.
Чтобы эту игру можно было обобщить на произвольную заданную размерность, удобно пересказать её как игру со спичками.
Игра с тремя кучками спичек. На столе лежат три кучки спичек. Двое играющих поочерёдно берут спички из этих кучек. За один ход можно взять любое число спичек, но только из одной кучки. Кто не может сделать ход, проигрывает (т.е. выигрывает тот, кто заберёт последнюю спичку).
Теперь игра просто обобщается на $n$-мерную бесконечную шахматную доску:
Игра «ним». На столе лежат $n$ кучек спичек. Двое играющих поочерёдно берут спички из этих кучек. За один ход можно взять любое число спичек, но только из одной кучки. Кто не может сделать ход, проигрывает (т.е. выигрывает тот, кто заберёт последнюю спичку).
Если ваш соперник не знает двоичной системы счисления, тогда вы смело можете делать большую ставку на вашу победу. Имея право выбрать, ходить первым или вторым, вы можете определить выигрышную стратегию посредством записи чисел (числа спичек в каждой кучке) в двоичной системе.
Видео-запись занятия кружка / 17 апреля, 2016 г. - Игры с графами. 24 апреля, 2016 г.
Представим, что турист приезжает на курорт и узнает, что экскурсоводы на этом курорте работают по следующим правилам.
Турист называет любой пункт назначения, а маршрут следования в этот пункт выбирает экскурсовод. Если турист уже видел хотя бы одно место по этому маршруту (за исключением начального и конечного пункта), тогда он он недоволен экскурсоводом и отказывается от его услуг, иначе турист платит экскурсоводу десять долларов и называет следующий пункт назначения (возможно, в котором они уже побывали). Так продолжается, пока у туриста есть деньги, либо до отказа от услуг экскурсовода.
В интересах экскурсовода - получить как можно больше денег, поэтому он будет петлять.
Пусть, например, турист из пункта 1 пожелал отправиться в пункт 5, затем - в пункт 3 и, наконец, в пункт 4 (как показано на рисунке ниже).
Если экскурсовод будет возить его по кратчайшим маршрутам, то уже на последнем отрезке пути турист разорвёт с ним контракт.
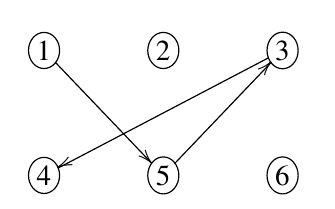
Если же экскурсовод поведёт туриста через окрестные деревни и темные переулки, он не только сможет довести его до пункта 4 и из него - в пункт 6 без пересечений маршрута, но после этого, даже если турист пожелает отправиться в пункт 2, экскурсовод без проблем выполнит эту задачу без угрозы разрыва контракта.
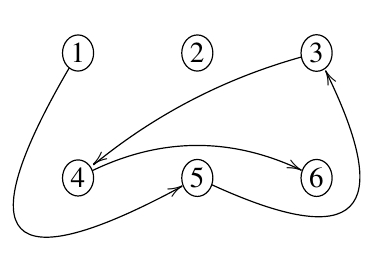
Какое наменьшее число достопримечательностей должен знать турист, чтобы разорвать контракт с хитрым экскурсоводом, если в некоторый момент стало понятно, что смотреть на курорте уже нечего? И сколько долларов туристу всё-таки придётся выложить при этом?
Мы попробуем найти ответы на эти вопросы.
- Шифрование методом поворотной решетки. 15 мая, 2016 г.
Пусть дан лист бумаги размером $2n \times 2m$ в клеточку - всего $2n \times 2m$ клеток. У такого листа бумаги всегда есть центр симметрии - точка пересечения двух прямых, разграничивающих лист на клетки, отражение относительно которой переводит лист в себя.
Вырежем на этом листе несколько окон произвольного размера, стороны которых проходят вдоль сторон клеток. Других ограничений на форму окон не накладывается. Мы считаем, что крайние клетки листа очерчены линиями со всех четырёх сторон.
Наложим лист с окнами на другой чистый лист такого же самого размера, но без окон. Через окна первого листа проставим крестики на втором листе - в каждую клеточку один крестик.
После чего повернём лист с окнами на $180$ градусов против часовой стрелки; его внешние стороны снова совпадут со сторонами второго листа. Далее посмотрим в окна. Может оказаться так, что через окна мы увидим некоторые отмеченные нами крестики, либо все крестики будут скрыты. Предположим, что крестиков не видно, тогда через окна снова можно в каждой видимой клеточке второго листа нарисовать крестик.
Теперь лист с окнами переворачиваем - задняя сторона окажется наверху. И опять накладываем на второй лист. Пусть снова оказалось так, что все отмеченные ранее крестики не видны. Это позволит нам продолжить беспрепятственно ставить новые крестики в окнах.
Далее, повернём лежащий лист с окнами снова на $180$ градусов против часовой стрелки. И будем считать, что нам снова повезло - в окнах мы видим только пустые клеточки, которые можно заполнить крестиками.
Если лист с окнами позволил проделать все вышеописанные операции, другими словами - при каждом повороте и развороте мы видим только пустые клетки, тогда такой лист называется поворотной решёткой. Поворотных решёток существует очень много. Одна из них, размера $6 \times 10$, показана на рисунке:
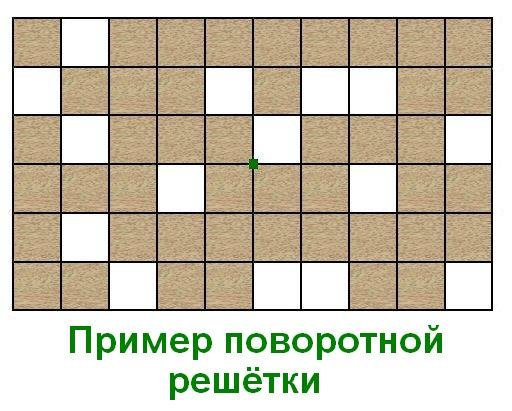
Способ шифрования «поворотной решёткой» заключается в том, что вместо крестиков в окна записываются буквы шифруемого текста. Как обычно, пишем слева направо, сверху вниз. В каждую клетку одну букву.
На следующих трёх рисунках мы видим первые три этапа заполнения окон при шифровке текста:
ШИФРРЕШЁТКАЯВЛЯЕТСЯЧАСТНЫМСЛУЧАЕМШИФРАМАРШРУТНОЙПЕРЕСТАНОВКИ 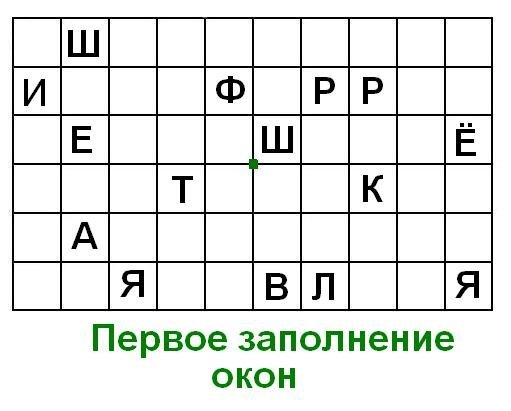

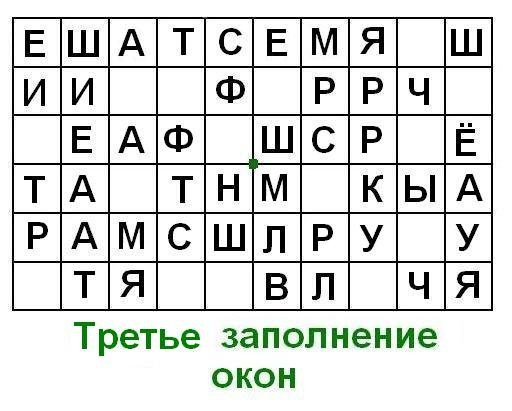
Ниже показан окончательный результат шифровки.

Если у вас есть ключ шифрования - поворотная решётка, то нетрудно прочитать зашифрованный текст.
Попробуйте расшифровать текст (см. страницу по этой ссылке), который закодирован способом «поворотная решётка», но неизвестно, какой именно поворотной решёткой шифровали.
|
Андрей Немытых, nemytykh@math.botik.ru |
Институт программных систем РАН,
г. Переславль-Залесский
http://www.botik.ru/pub/local/scp/refal5/
