1.3 Pattern Matching
Pattern expressions (or just patterns) of Refal
differ from object expressions in that they may include free variables.
Here are a few examples of free variables:
e.1 e.Data1 e.data1 s.X s.Free-var t.1 t.25
A free variable is formed by a type sign, a dot, and an index. The index
of a variable is an identifier or a whole number.
There are three type signs. They are
represented by the lower-case letters s
, t
, and e
;
the corresponding variables are referred to as s-, t-, and
e-variables. The difference between them is in the sets of their admissible
values. An s-variable can take only a single symbol as its value.
A t-variable takes any term as its value (recall that a term is either
a symbol or an expression in structure brackets).
An e-variable can take any expression as its value.
A pattern expression can be viewed
as a set of object expressions which are obtained by substituting
admissible values for all variables. Thus the pattern A e.1represents
the set of all object expressions starting with the symbol A
. All
entries of the same variable must be replaced by the same value. The pattern
s.1 e.2 s.1 can be seen as the set of all object expressions which
start and end with the same symbol and have at least two symbols.
But pattern expressions also have another function: they describe a
decomposition of an object expression, during which the
variables in the pattern are identified with some parts of the object
expression, i.e., take certain values. Viewed in this way, A e.1 is
a procedure which checks that the first symbol of a given object expression
is A
, and assigns the remaining part of it to e.1
as its value.
This procedure is known as pattern matching.
Given an object expression
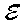 and a pattern expression
and a pattern expression
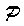 , we denote the
operation of matching
, we denote the
operation of matching
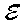 to
to
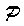 as
as
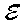 :
:
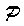 where the colon is one more
special sign of Refal; the matching sign. We also say that
where the colon is one more
special sign of Refal; the matching sign. We also say that
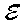 is being
recognized as (a particular case of)
is being
recognized as (a particular case of)
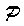 .
In the pair
.
In the pair
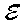 :
:
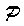 we call
we call
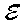 the argument and
the argument and
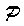 the pattern
of the matching operation.
the pattern
of the matching operation.
If there exists a
substitution
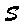 for the variables in
for the variables in
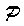 such that applying
such that applying
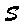 to
to
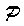 yields
yields
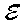 , then we say that the matching, or recognition, is successful.
The variables in
, then we say that the matching, or recognition, is successful.
The variables in
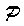 take on the values prescribed by
take on the values prescribed by
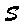 . Otherwise,
the matching fails. If there is more than one way of assigning values
to the free variables in the pattern in order to achieve matching, then the one is
chosen in which the leftmost e-variable takes the shortest value. If this
does not resolve the ambiguity, the same selection is done on the next
(from the left) e-variable, etc. In other words, when we perform matching,
we scan the argument
. Otherwise,
the matching fails. If there is more than one way of assigning values
to the free variables in the pattern in order to achieve matching, then the one is
chosen in which the leftmost e-variable takes the shortest value. If this
does not resolve the ambiguity, the same selection is done on the next
(from the left) e-variable, etc. In other words, when we perform matching,
we scan the argument
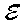 from left to right and pick the first
successful match of
from left to right and pick the first
successful match of
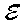 to
to
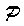 .
.
Here are a few examples. The matching
A B C : A e.1
succeeds with e.1
taking the value B C . The matching
('ABC') '++' : s.X e.1
fails, because the left parenthesis is not a symbol, so it cannot
be matched to s.X
. Neither can it be ignored. However,
('ABC') '++' : (s.X e.1) e.Out
succeeds, with s.X
becoming 'A', e.1
becoming 'BC', and e.Out
becoming '++'.
The recognition of '++'
as s.1 e.2 s.1 succeeds —
with s.1
taking the value '+'
and e.2
the
empty expression. But
'+' : s.1 e.2 s.1
fails.
The following matching:
A B '+' C '+' D E F : e.1 '+' e.2
is an example of a situation where there is more than one way
to assign values for matching. According to the definition above,
the symbol '+'
in the pattern will be identified with the first
symbol '+'
in the argument (the left-to-right matching).
Thus e.1
will take A B
as its value and e.2
will
become C '+' D E F.
In the following example:
A B '-' (C '+' D E F) : e.1 '+' e.2
the matching will fail because the only symbol '+'
of
the argument is inside
parentheses. To match it to the '+'
in the pattern, we would have
to assign to e.1
and e.2
some values that were unbalanced
with respect to parentheses, and this is impossible. Refal takes structure brackets
very seriously. Parts of expressions that are not expressions themselves
cannot be treated separately in any context.
Exercise 1.3
Write patterns that can be described in words as follows:
(a) an expression ending with two identical symbols;
(b) an expression which contains at least two identical terms
on the top level of structure; (c) a non-empty expression.
Exercise 1.4
Find the results of the following matchings:
(a) 'abbab' : e.1 t.X t.X e.2
(b) 'ab(b)ab' : e.1 t.X t.X e.2
(c) A(B) C D (A (B)) : e.6 e.4(e.6)
(d) '16 0' : 16 e.Z
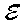 and a pattern expression
and a pattern expression
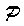 , we denote the
operation of matching
, we denote the
operation of matching
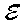 to
to
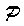 as
as
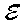 :
:
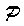 where the colon is one more
special sign of Refal; the matching sign. We also say that
where the colon is one more
special sign of Refal; the matching sign. We also say that
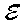 is being
recognized as (a particular case of)
is being
recognized as (a particular case of)
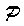 .
In the pair
.
In the pair
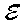 :
:
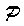 we call
we call
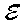 the argument and
the argument and
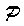 the pattern
of the matching operation.
the pattern
of the matching operation.
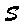 for the variables in
for the variables in